Acceleration Strategies for MR-STAT: Achieving High-Resolution Reconstructions on a Desktop PC within 3 minutes
Paper and Code
May 04, 2022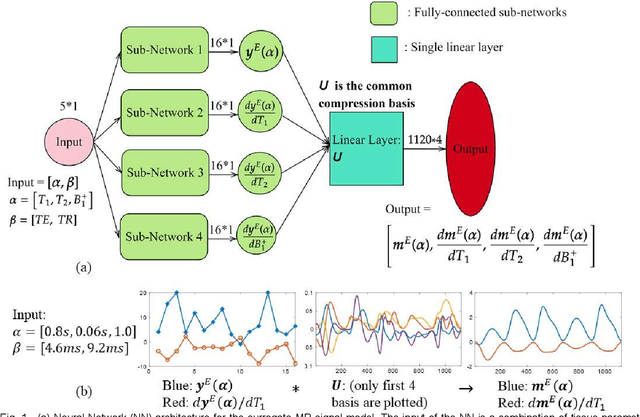
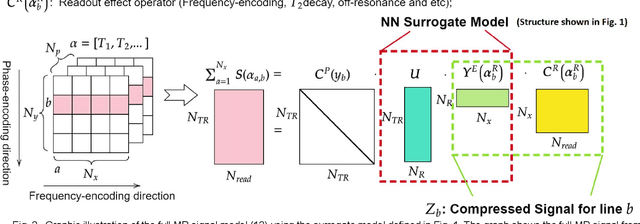
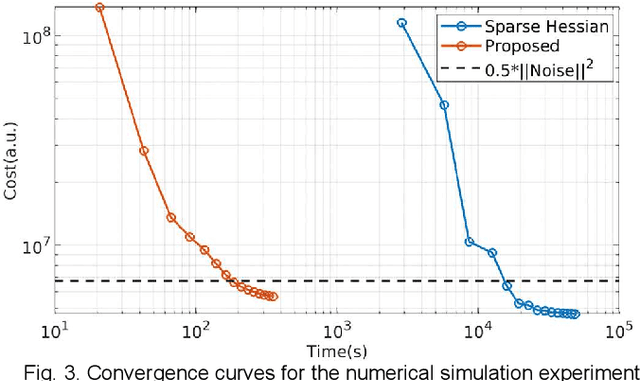
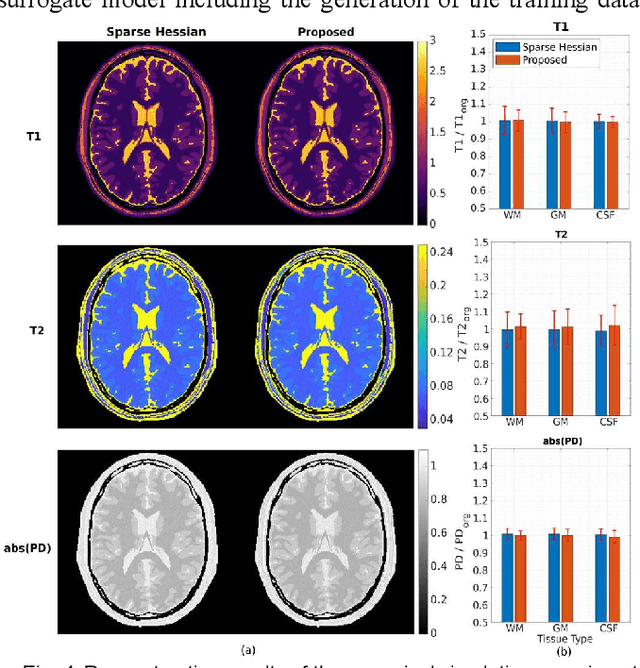
MR-STAT is an emerging quantitative magnetic resonance imaging technique which aims at obtaining multi-parametric tissue parameter maps from single short scans. It describes the relationship between the spatial-domain tissue parameters and the time-domain measured signal by using a comprehensive, volumetric forward model. The MR-STAT reconstruction solves a large-scale nonlinear problem, thus is very computationally challenging. In previous work, MR-STAT reconstruction using Cartesian readout data was accelerated by approximating the Hessian matrix with sparse, banded blocks, and can be done on high performance CPU clusters with tens of minutes. In the current work, we propose an accelerated Cartesian MR-STAT algorithm incorporating two different strategies: firstly, a neural network is trained as a fast surrogate to learn the magnetization signal not only in the full time-domain but also in the compressed lowrank domain; secondly, based on the surrogate model, the Cartesian MR-STAT problem is re-formulated and split into smaller sub-problems by the alternating direction method of multipliers. The proposed method substantially reduces the computational requirements for runtime and memory. Simulated and in-vivo balanced MR-STAT experiments show similar reconstruction results using the proposed algorithm compared to the previous sparse Hessian method, and the reconstruction times are at least 40 times shorter. Incorporating sensitivity encoding and regularization terms is straightforward, and allows for better image quality with a negligible increase in reconstruction time. The proposed algorithm could reconstruct both balanced and gradient-spoiled in-vivo data within 3 minutes on a desktop PC, and could thereby facilitate the translation of MR-STAT in clinical settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge