A Unitary Weights Based One-Iteration Quantum Perceptron Algorithm for Non-Ideal Training Sets
Paper and Code
Sep 23, 2023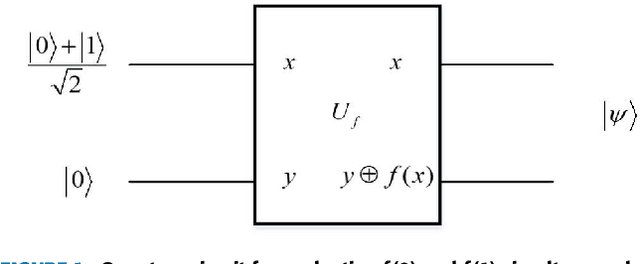
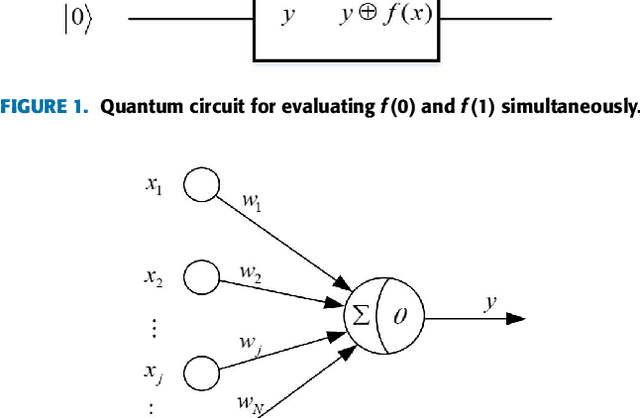
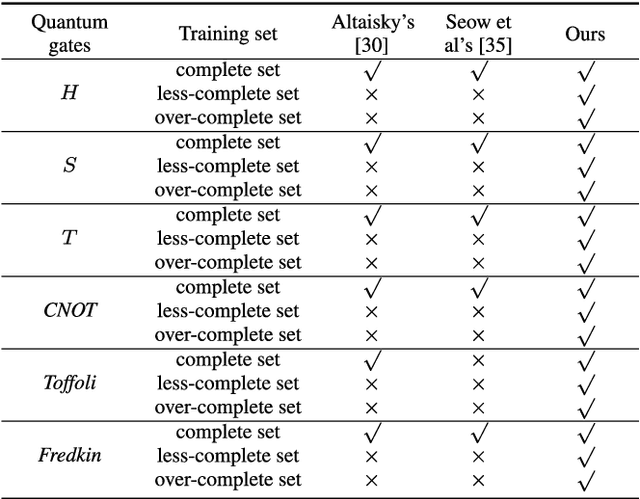
In order to solve the problem of non-ideal training sets (i.e., the less-complete or over-complete sets) and implement one-iteration learning, a novel efficient quantum perceptron algorithm based on unitary weights is proposed, where the singular value decomposition of the total weight matrix from the training set is calculated to make the weight matrix to be unitary. The example validation of quantum gates {H, S, T, CNOT, Toffoli, Fredkin} shows that our algorithm can accurately implement arbitrary quantum gates within one iteration. The performance comparison between our algorithm and other quantum perceptron algorithms demonstrates the advantages of our algorithm in terms of applicability, accuracy, and availability. For further validating the applicability of our algorithm, a quantum composite gate which consists of several basic quantum gates is also illustrated.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge