A Unified Framework for Implicit Sinkhorn Differentiation
Paper and Code
May 13, 2022
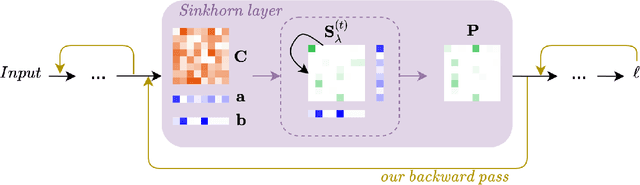

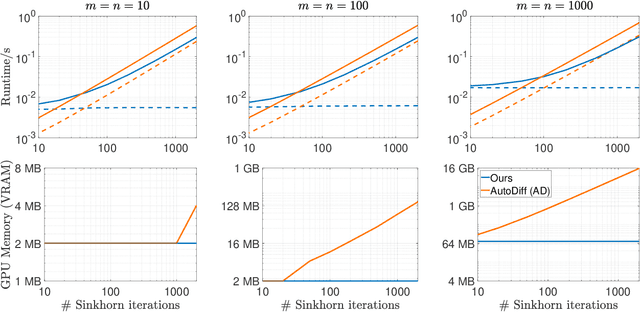
The Sinkhorn operator has recently experienced a surge of popularity in computer vision and related fields. One major reason is its ease of integration into deep learning frameworks. To allow for an efficient training of respective neural networks, we propose an algorithm that obtains analytical gradients of a Sinkhorn layer via implicit differentiation. In comparison to prior work, our framework is based on the most general formulation of the Sinkhorn operator. It allows for any type of loss function, while both the target capacities and cost matrices are differentiated jointly. We further construct error bounds of the resulting algorithm for approximate inputs. Finally, we demonstrate that for a number of applications, simply replacing automatic differentiation with our algorithm directly improves the stability and accuracy of the obtained gradients. Moreover, we show that it is computationally more efficient, particularly when resources like GPU memory are scarce.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge