A Unified Approach to Reinforcement Learning, Quantal Response Equilibria, and Two-Player Zero-Sum Games

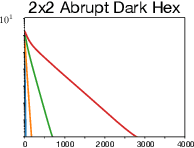
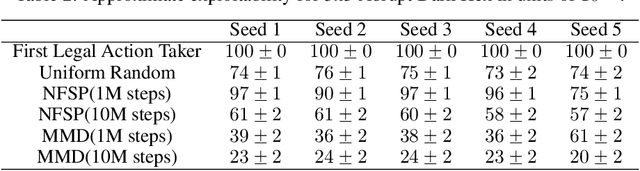
Algorithms designed for single-agent reinforcement learning (RL) generally fail to converge to equilibria in two-player zero-sum (2p0s) games. Conversely, game-theoretic algorithms for approximating Nash and quantal response equilibria (QREs) in 2p0s games are not typically competitive for RL and can be difficult to scale. As a result, algorithms for these two cases are generally developed and evaluated separately. In this work, we show that a single algorithm -- a simple extension to mirror descent with proximal regularization that we call magnetic mirror descent (MMD) -- can produce strong results in both settings, despite their fundamental differences. From a theoretical standpoint, we prove that MMD converges linearly to QREs in extensive-form games -- this is the first time linear convergence has been proven for a first order solver. Moreover, applied as a tabular Nash equilibrium solver via self-play, we show empirically that MMD produces results competitive with CFR in both normal-form and extensive-form games with full feedback (this is the first time that a standard RL algorithm has done so) and also that MMD empirically converges in black-box feedback settings. Furthermore, for single-agent deep RL, on a small collection of Atari and Mujoco games, we show that MMD can produce results competitive with those of PPO. Lastly, for multi-agent deep RL, we show MMD can outperform NFSP in 3x3 Abrupt Dark Hex.