A Two-Stage Imaging Framework Combining CNN and Physics-Informed Neural Networks for Full-Inverse Tomography: A Case Study in Electrical Impedance Tomography (EIT)
Paper and Code
Jul 25, 2024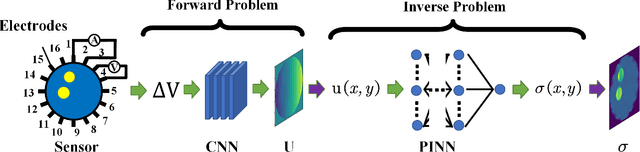
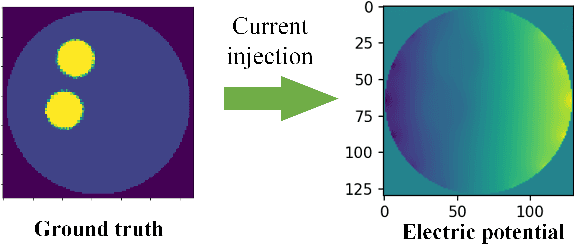
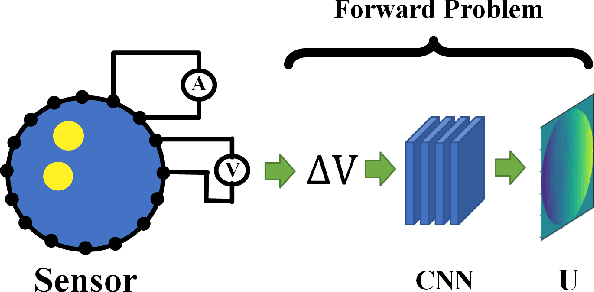
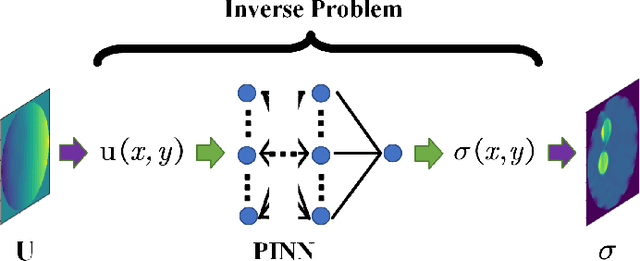
Physics-Informed Neural Networks (PINNs) are a machine learning technique for solving partial differential equations (PDEs) by incorporating PDEs as loss terms in neural networks and minimizing the loss function during training. Tomographic imaging, a method to reconstruct internal properties from external measurement data, is highly complex and ill-posed, making it an inverse problem. Recently, PINNs have shown significant potential in computational fluid dynamics (CFD) and have advantages in solving inverse problems. However, existing research has primarily focused on semi-inverse Electrical Impedance Tomography (EIT), where internal electric potentials are accessible. The practical full inverse EIT problem, where only boundary voltage measurements are available, remains challenging. To address this, we propose a two-stage hybrid learning framework combining Convolutional Neural Networks (CNNs) and PINNs to solve the full inverse EIT problem. This framework integrates data-driven and model-driven approaches, combines supervised and unsupervised learning, and decouples the forward and inverse problems within the PINN framework in EIT. Stage I: a U-Net constructs an end-to-end mapping from boundary voltage measurements to the internal potential distribution using supervised learning. Stage II: a Multilayer Perceptron (MLP)-based PINN takes the predicted internal potentials as input to solve for the conductivity distribution through unsupervised learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge