A Twin Neural Model for Uplift
Paper and Code
May 11, 2021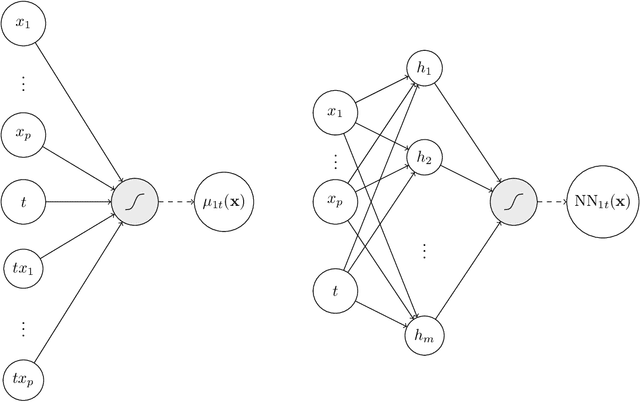
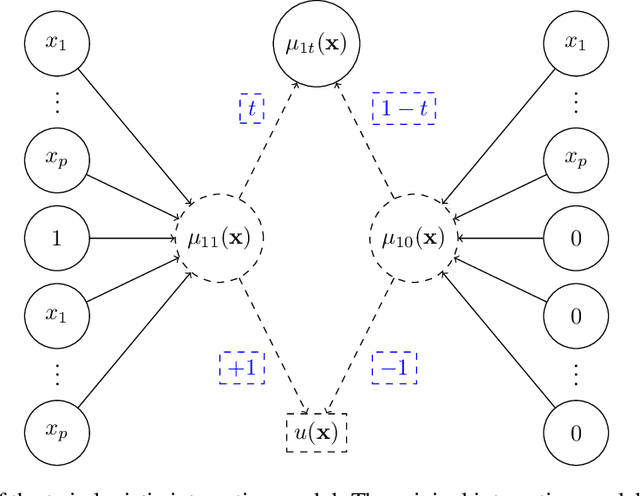
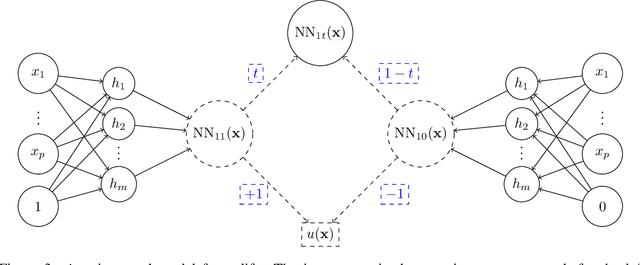
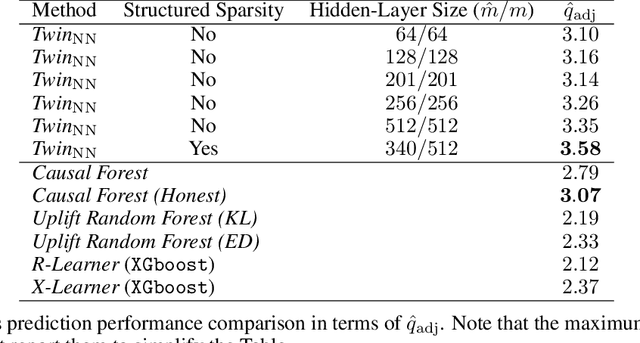
Uplift is a particular case of conditional treatment effect modeling. Such models deal with cause-and-effect inference for a specific factor, such as a marketing intervention or a medical treatment. In practice, these models are built on individual data from randomized clinical trials where the goal is to partition the participants into heterogeneous groups depending on the uplift. Most existing approaches are adaptations of random forests for the uplift case. Several split criteria have been proposed in the literature, all relying on maximizing heterogeneity. However, in practice, these approaches are prone to overfitting. In this work, we bring a new vision to uplift modeling. We propose a new loss function defined by leveraging a connection with the Bayesian interpretation of the relative risk. Our solution is developed for a specific twin neural network architecture allowing to jointly optimize the marginal probabilities of success for treated and control individuals. We show that this model is a generalization of the uplift logistic interaction model. We modify the stochastic gradient descent algorithm to allow for structured sparse solutions. This helps training our uplift models to a great extent. We show our proposed method is competitive with the state-of-the-art in simulation setting and on real data from large scale randomized experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge