A Theoretical View of Linear Backpropagation and Its Convergence
Paper and Code
Dec 21, 2021
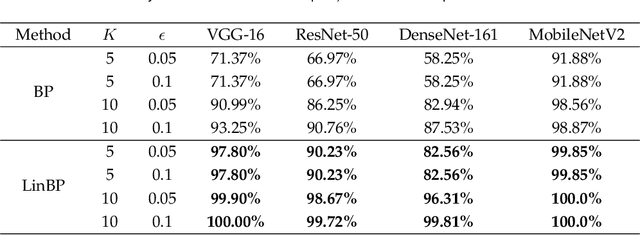


Backpropagation is widely used for calculating gradients in deep neural networks (DNNs). Applied often along with stochastic gradient descent (SGD) or its variants, backpropagation is considered as a de-facto choice in a variety of machine learning tasks including DNN training and adversarial attack/defense. Recently, a linear variant of BP named LinBP was introduced for generating more transferable adversarial examples for black-box adversarial attacks, by Guo et al. Yet, it has not been theoretically studied and the convergence analysis of such a method is lacking. This paper serves as a complement and somewhat an extension to Guo et al.'s paper, by providing theoretical analyses on LinBP in neural-network-involved learning tasks including adversarial attack and model training. We demonstrate that, somewhat surprisingly, LinBP can lead to faster convergence in these tasks in the same hyper-parameter settings, compared to BP. We confirm our theoretical results with extensive experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge