A Spectral Approach for the Design of Experiments: Design, Analysis and Algorithms
Paper and Code
Dec 16, 2017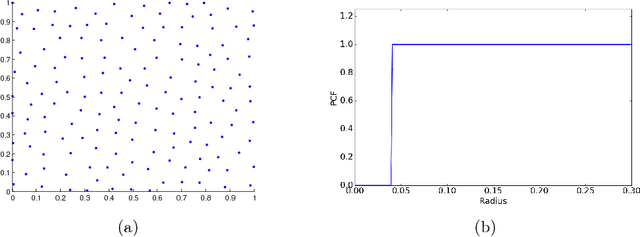

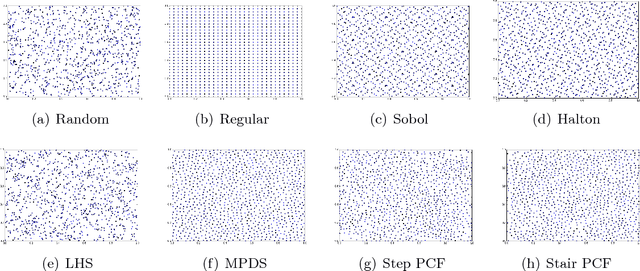
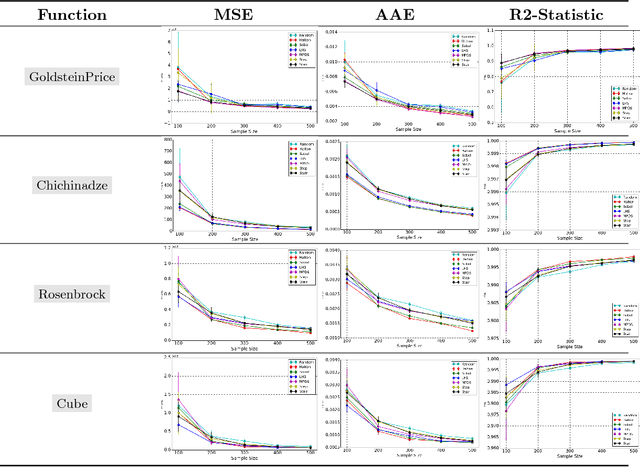
This paper proposes a new approach to construct high quality space-filling sample designs. First, we propose a novel technique to quantify the space-filling property and optimally trade-off uniformity and randomness in sample designs in arbitrary dimensions. Second, we connect the proposed metric (defined in the spatial domain) to the objective measure of the design performance (defined in the spectral domain). This connection serves as an analytic framework for evaluating the qualitative properties of space-filling designs in general. Using the theoretical insights provided by this spatial-spectral analysis, we derive the notion of optimal space-filling designs, which we refer to as space-filling spectral designs. Third, we propose an efficient estimator to evaluate the space-filling properties of sample designs in arbitrary dimensions and use it to develop an optimization framework to generate high quality space-filling designs. Finally, we carry out a detailed performance comparison on two different applications in 2 to 6 dimensions: a) image reconstruction and b) surrogate modeling on several benchmark optimization functions and an inertial confinement fusion (ICF) simulation code. We demonstrate that the propose spectral designs significantly outperform existing approaches especially in high dimensions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge