A Simple and Scalable Shape Representation for 3D Reconstruction
Paper and Code
May 10, 2020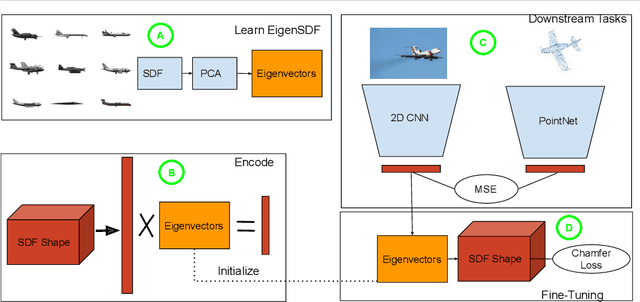
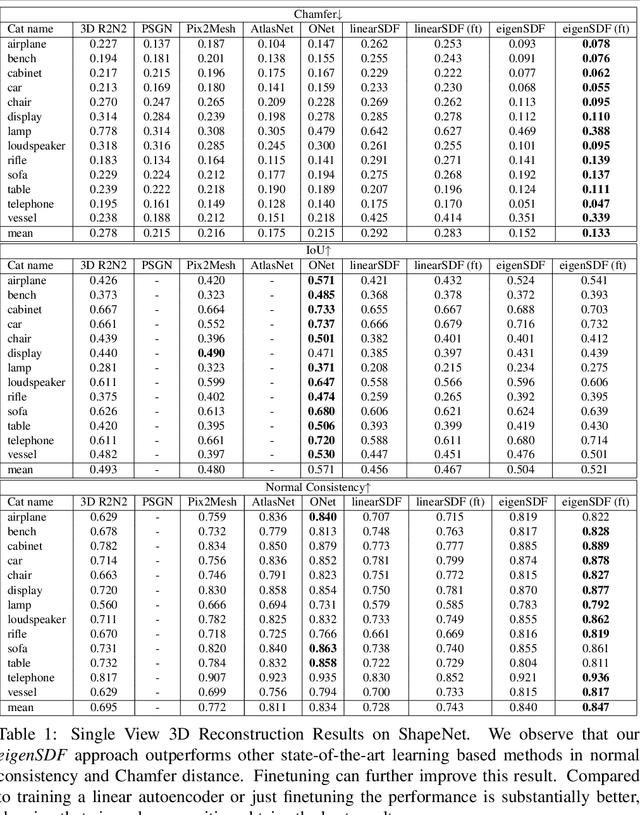
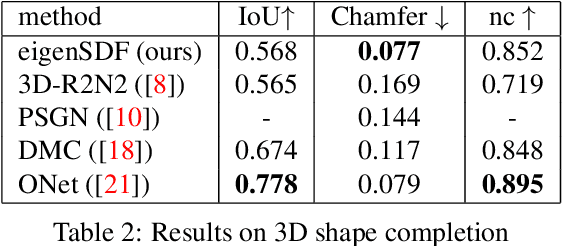
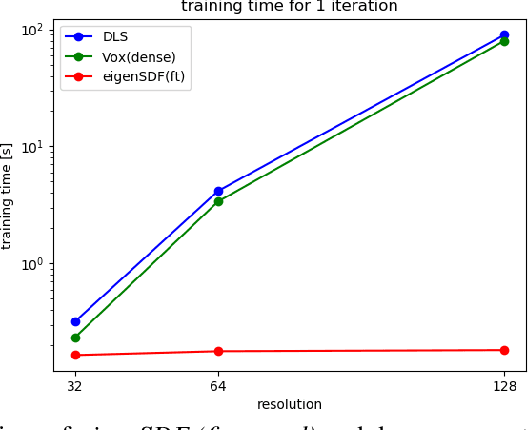
Deep learning applied to the reconstruction of 3D shapes has seen growing interest. A popular approach to 3D reconstruction and generation in recent years has been the CNN encoder-decoder model usually applied in voxel space. However, this often scales very poorly with the resolution limiting the effectiveness of these models. Several sophisticated alternatives for decoding to 3D shapes have been proposed typically relying on complex deep learning architectures for the decoder model. In this work, we show that this additional complexity is not necessary, and that we can actually obtain high quality 3D reconstruction using a linear decoder, obtained from principal component analysis on the signed distance function (SDF) of the surface. This approach allows easily scaling to larger resolutions. We show in multiple experiments that our approach is competitive with state-of-the-art methods. It also allows the decoder to be fine-tuned on the target task using a loss designed specifically for SDF transforms, obtaining further gains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge