A Rotated Hyperbolic Wrapped Normal Distribution for Hierarchical Representation Learning

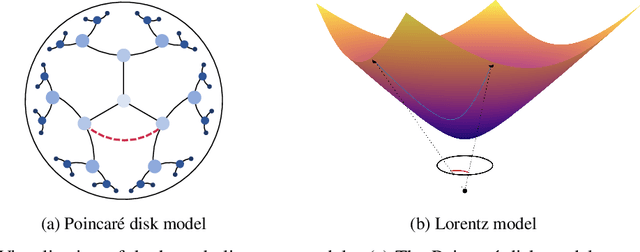
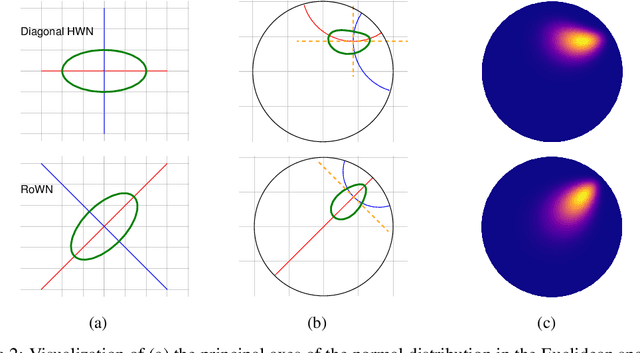
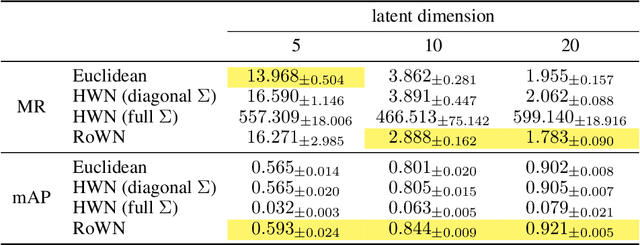
We present a rotated hyperbolic wrapped normal distribution (RoWN), a simple yet effective alteration of a hyperbolic wrapped normal distribution (HWN). The HWN expands the domain of probabilistic modeling from Euclidean to hyperbolic space, where a tree can be embedded with arbitrary low distortion in theory. In this work, we analyze the geometric properties of the diagonal HWN, a standard choice of distribution in probabilistic modeling. The analysis shows that the distribution is inappropriate to represent the data points at the same hierarchy level through their angular distance with the same norm in the Poincar\'e disk model. We then empirically verify the presence of limitations of HWN, and show how RoWN, the newly proposed distribution, can alleviate the limitations on various hierarchical datasets, including noisy synthetic binary tree, WordNet, and Atari 2600 Breakout.