A Regularization Approach for Prediction of Edges and Node Features in Dynamic Graphs
Paper and Code
Mar 24, 2012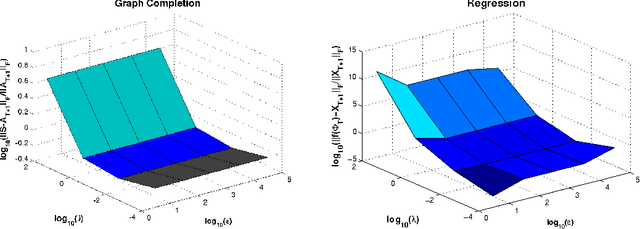

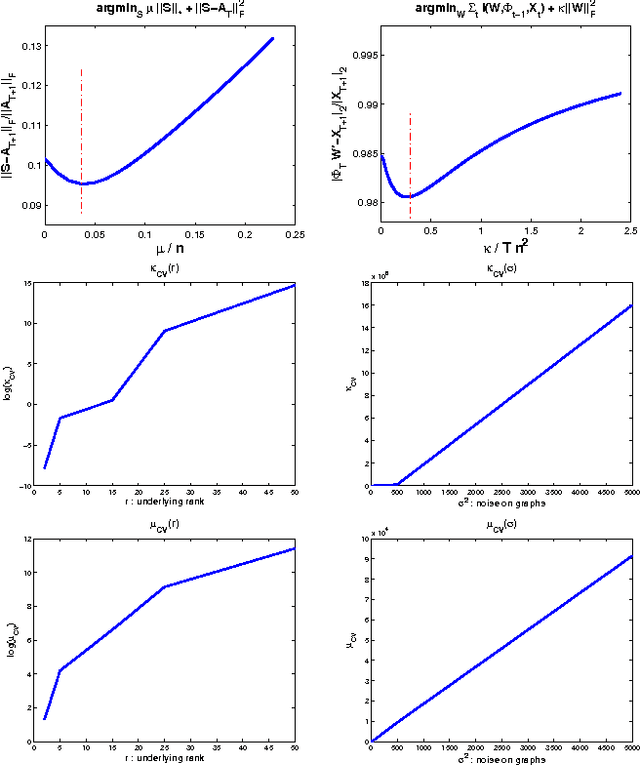
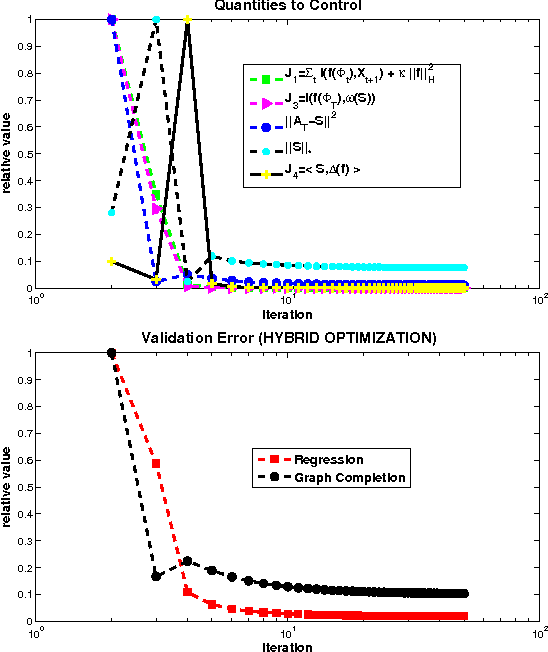
We consider the two problems of predicting links in a dynamic graph sequence and predicting functions defined at each node of the graph. In many applications, the solution of one problem is useful for solving the other. Indeed, if these functions reflect node features, then they are related through the graph structure. In this paper, we formulate a hybrid approach that simultaneously learns the structure of the graph and predicts the values of the node-related functions. Our approach is based on the optimization of a joint regularization objective. We empirically test the benefits of the proposed method with both synthetic and real data. The results indicate that joint regularization improves prediction performance over the graph evolution and the node features.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge