A New Design of Cache-aided Multiuser Private Information Retrieval with Uncoded Prefetching
Paper and Code
Feb 03, 2021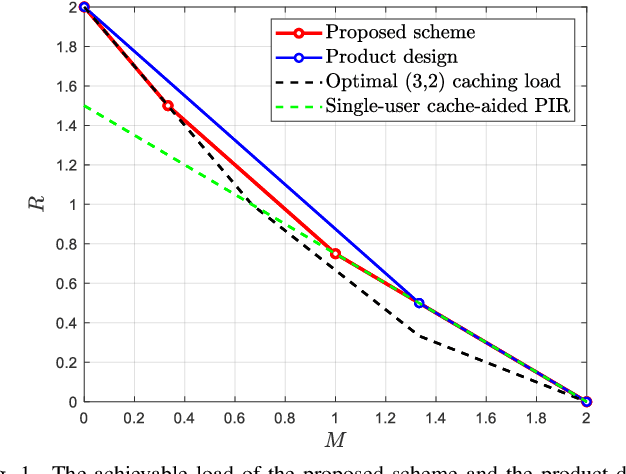
In the problem of cache-aided multiuser private information retrieval (MuPIR), a set of $K_{\rm u}$ cache-equipped users wish to privately download a set of messages from $N$ distributed databases each holding a library of $K$ messages. The system works in two phases: {\it cache placement (prefetching) phase} in which the users fill up their cache memory, and {\it private delivery phase} in which the users' demands are revealed and they download an answer from each database so that the their desired messages can be recovered while each individual database learns nothing about the identities of the requested messages. The goal is to design the placement and the private delivery phases such that the \emph{load}, which is defined as the total number of downloaded bits normalized by the message size, is minimized given any user memory size. This paper considers the MuPIR problem with two messages, arbitrary number of users and databases where uncoded prefetching is assumed, i.e., the users directly copy some bits from the library as their cached contents. We propose a novel MuPIR scheme inspired by the Maddah-Ali and Niesen (MAN) coded caching scheme. The proposed scheme achieves lower load than any existing schemes, especially the product design (PD), and is shown to be optimal within a factor of $8$ in general and exactly optimal at very high or low memory regime.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge