A Multi-body Tracking Framework -- From Rigid Objects to Kinematic Structures
Paper and Code
Aug 02, 2022
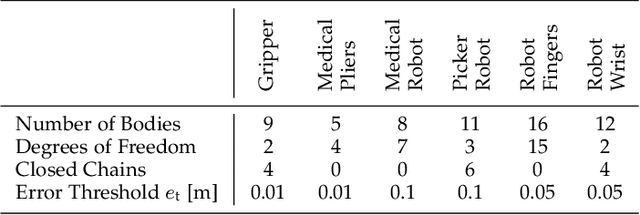
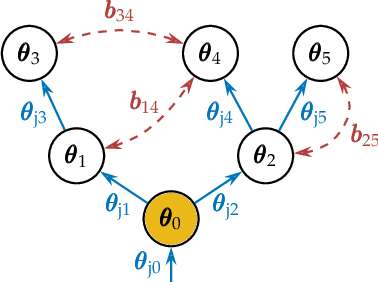
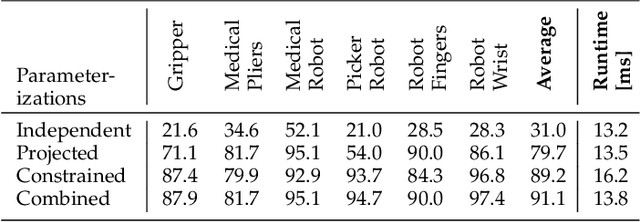
Kinematic structures are very common in the real world. They range from simple articulated objects to complex mechanical systems. However, despite their relevance, most model-based 3D tracking methods only consider rigid objects. To overcome this limitation, we propose a flexible framework that allows the extension of existing 6DoF algorithms to kinematic structures. Our approach focuses on methods that employ Newton-like optimization techniques, which are widely used in object tracking. The framework considers both tree-like and closed kinematic structures and allows a flexible configuration of joints and constraints. To project equations from individual rigid bodies to a multi-body system, Jacobians are used. For closed kinematic chains, a novel formulation that features Lagrange multipliers is developed. In a detailed mathematical proof, we show that our constraint formulation leads to an exact kinematic solution and converges in a single iteration. Based on the proposed framework, we extend ICG, which is a state-of-the-art rigid object tracking algorithm, to multi-body tracking. For the evaluation, we create a highly-realistic synthetic dataset that features a large number of sequences and various robots. Based on this dataset, we conduct a wide variety of experiments that demonstrate the excellent performance of the developed framework and our multi-body tracker.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge