A Higher-Order Kolmogorov-Smirnov Test
Paper and Code
Mar 24, 2019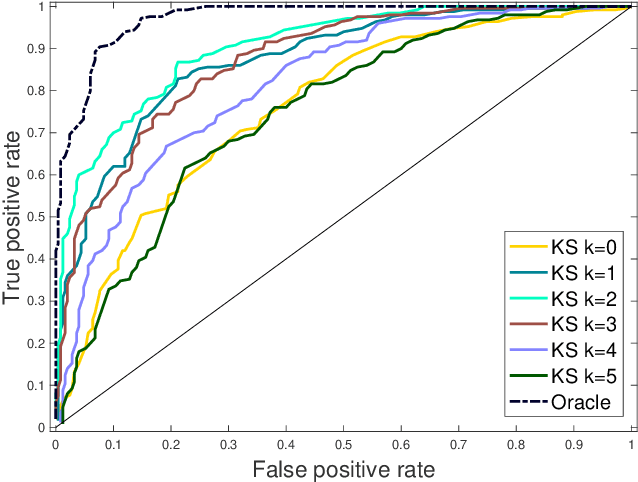
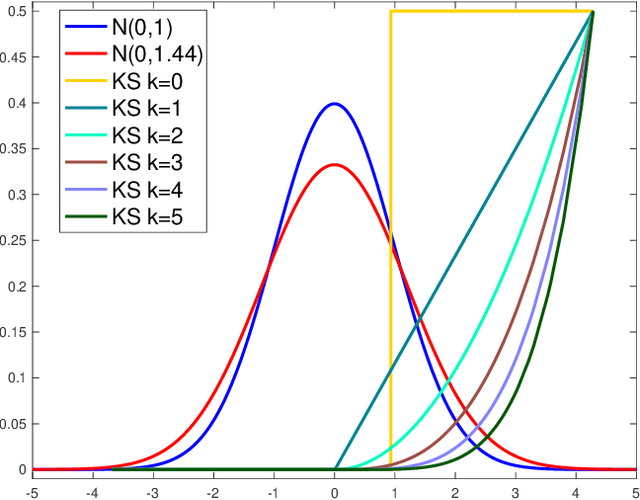
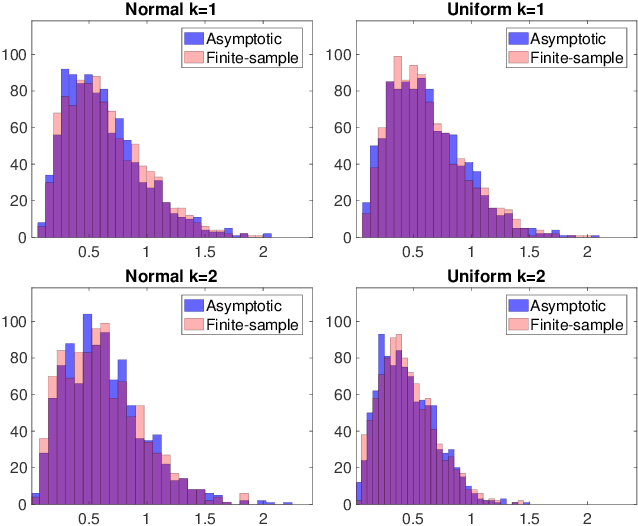
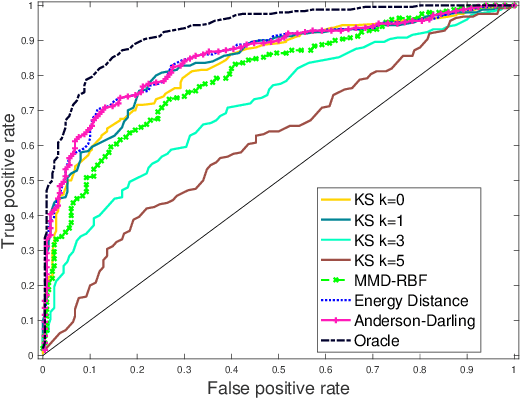
We present an extension of the Kolmogorov-Smirnov (KS) two-sample test, which can be more sensitive to differences in the tails. Our test statistic is an integral probability metric (IPM) defined over a higher-order total variation ball, recovering the original KS test as its simplest case. We give an exact representer result for our IPM, which generalizes the fact that the original KS test statistic can be expressed in equivalent variational and CDF forms. For small enough orders ($k \leq 5$), we develop a linear-time algorithm for computing our higher-order KS test statistic; for all others ($k \geq 6$), we give a nearly linear-time approximation. We derive the asymptotic null distribution for our test, and show that our nearly linear-time approximation shares the same asymptotic null. Lastly, we complement our theory with numerical studies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge