A Granular Sieving Algorithm for Deterministic Global Optimization
Paper and Code
Jul 14, 2021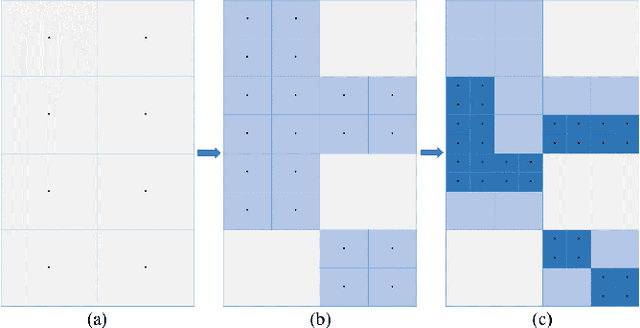

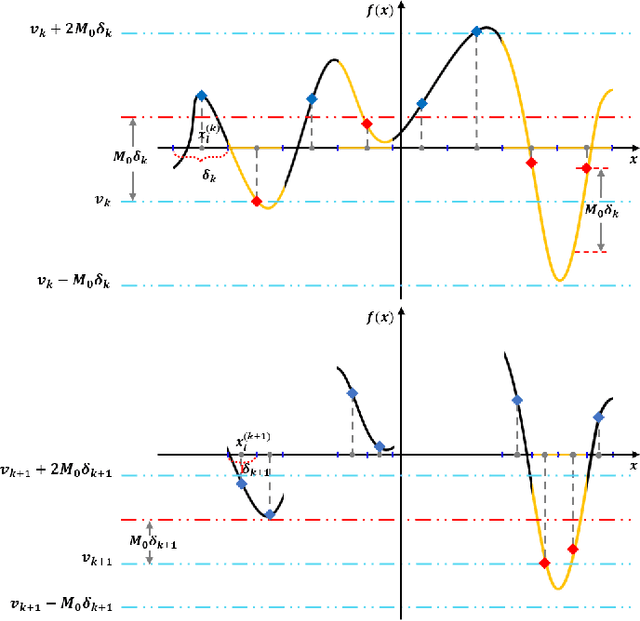
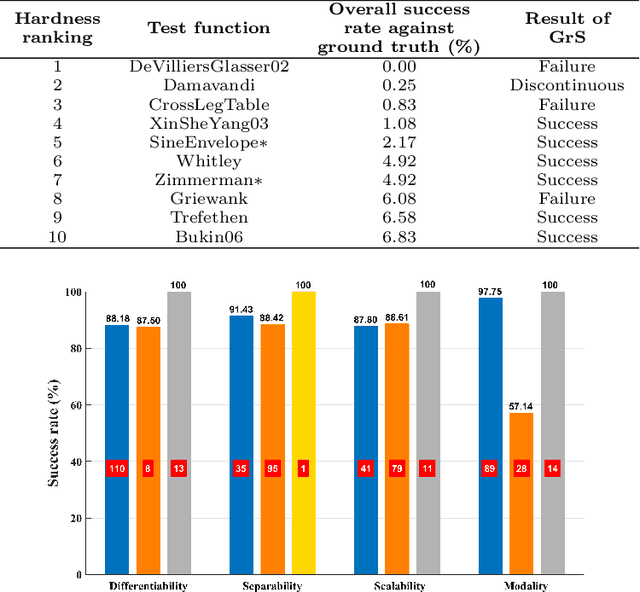
A gradient-free deterministic method is developed to solve global optimization problems for Lipschitz continuous functions defined in arbitrary path-wise connected compact sets in Euclidean spaces. The method can be regarded as granular sieving with synchronous analysis in both the domain and range of the objective function. With straightforward mathematical formulation applicable to both univariate and multivariate objective functions, the global minimum value and all the global minimizers are located through two decreasing sequences of compact sets in, respectively, the domain and range spaces. The algorithm is easy to implement with moderate computational cost. The method is tested against extensive benchmark functions in the literature. The experimental results show remarkable effectiveness and applicability of the algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge