A Generic Coordinate Descent Framework for Learning from Implicit Feedback
Paper and Code
Nov 15, 2016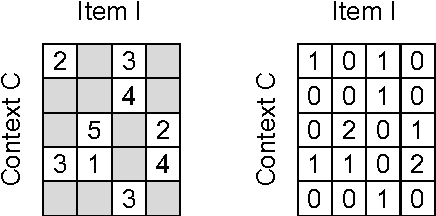
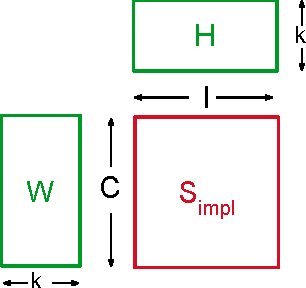
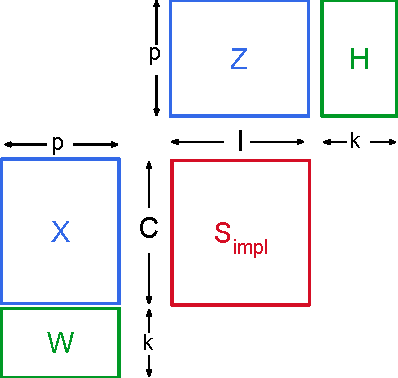
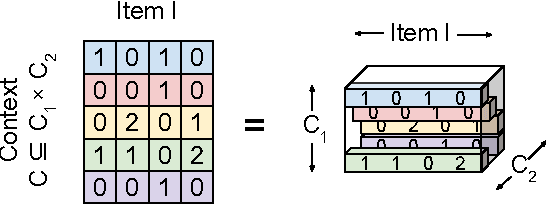
In recent years, interest in recommender research has shifted from explicit feedback towards implicit feedback data. A diversity of complex models has been proposed for a wide variety of applications. Despite this, learning from implicit feedback is still computationally challenging. So far, most work relies on stochastic gradient descent (SGD) solvers which are easy to derive, but in practice challenging to apply, especially for tasks with many items. For the simple matrix factorization model, an efficient coordinate descent (CD) solver has been previously proposed. However, efficient CD approaches have not been derived for more complex models. In this paper, we provide a new framework for deriving efficient CD algorithms for complex recommender models. We identify and introduce the property of k-separable models. We show that k-separability is a sufficient property to allow efficient optimization of implicit recommender problems with CD. We illustrate this framework on a variety of state-of-the-art models including factorization machines and Tucker decomposition. To summarize, our work provides the theory and building blocks to derive efficient implicit CD algorithms for complex recommender models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge