A General Large Neighborhood Search Framework for Solving Integer Programs
Paper and Code
Mar 29, 2020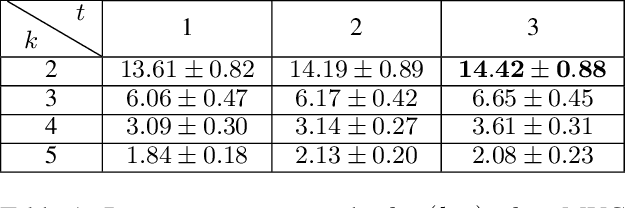
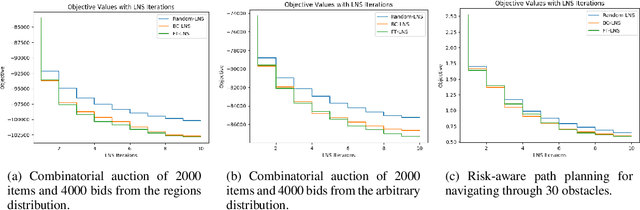
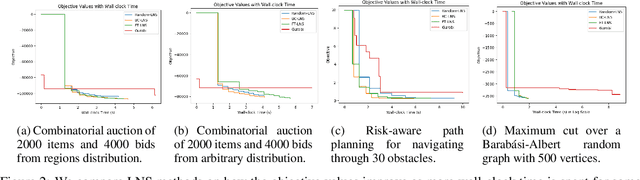

This paper studies how to design abstractions of large-scale combinatorial optimization problems that can leverage existing state-of-the-art solvers in general purpose ways, and that are amenable to data-driven design. The goal is to arrive at new approaches that can reliably outperform existing solvers in wall-clock time. We focus on solving integer programs, and ground our approach in the large neighborhood search (LNS) paradigm, which iteratively chooses a subset of variables to optimize while leaving the remainder fixed. The appeal of LNS is that it can easily use any existing solver as a subroutine, and thus can inherit the benefits of carefully engineered heuristic approaches and their software implementations. We also show that one can learn a good neighborhood selector from training data. Through an extensive empirical validation, we demonstrate that our LNS framework can significantly outperform, in wall-clock time, compared to state-of-the-art commercial solvers such as Gurobi.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge