A Fast Proximal Point Method for Computing Wasserstein Distance

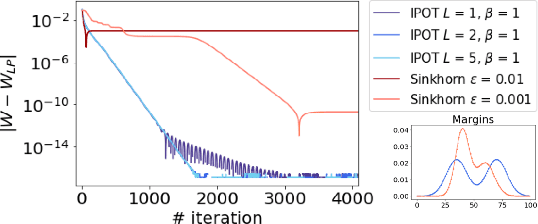
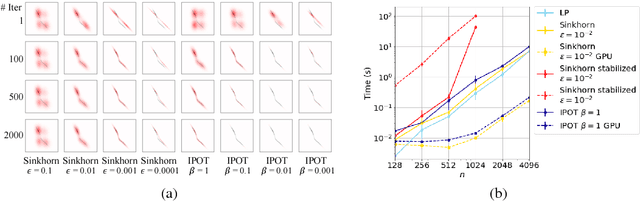
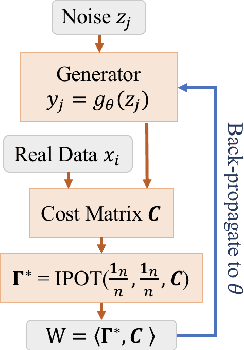
Wasserstein distance plays increasingly important roles in machine learning, stochastic programming and image processing. Major efforts have been under way to address its high computational complexity, some leading to approximate or regularized variations such as Sinkhorn distance. However, as we will demonstrate, regularized variations with large regularization parameter will degradate the performance in several important machine learning applications, and small regularization parameter will fail due to numerical stability issues with existing algorithms. We address this challenge by developing an Inexact Proximal point method for Optimal Transport (IPOT) with the proximal operator approximately evaluated at each iteration using projections to the probability simplex. We prove the algorithm has linear convergence rate. We also apply IPOT to learning generative models, and generalize the idea of IPOT to a new method for computing Wasserstein barycenter.