A Differentiable Loss Function for Learning Heuristics in A*
Paper and Code
Sep 12, 2022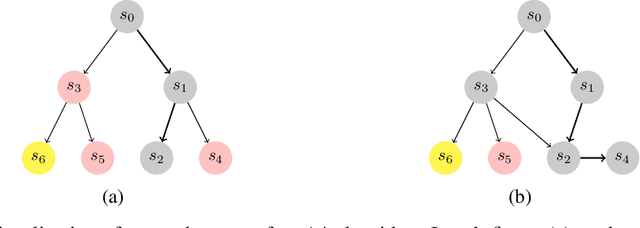
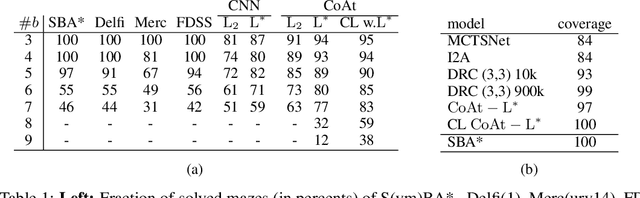
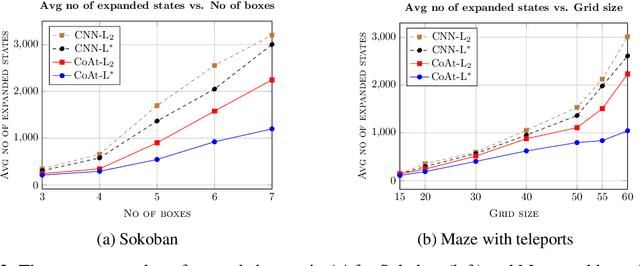
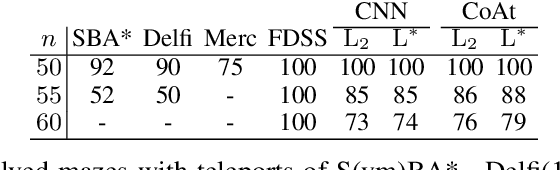
Optimization of heuristic functions for the A* algorithm, realized by deep neural networks, is usually done by minimizing square root loss of estimate of the cost to goal values. This paper argues that this does not necessarily lead to a faster search of A* algorithm since its execution relies on relative values instead of absolute ones. As a mitigation, we propose a L* loss, which upper-bounds the number of excessively expanded states inside the A* search. The L* loss, when used in the optimization of state-of-the-art deep neural networks for automated planning in maze domains like Sokoban and maze with teleports, significantly improves the fraction of solved problems, the quality of founded plans, and reduces the number of expanded states to approximately 50%
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge