A deep-structured fully-connected random field model for structured inference
Paper and Code
May 27, 2015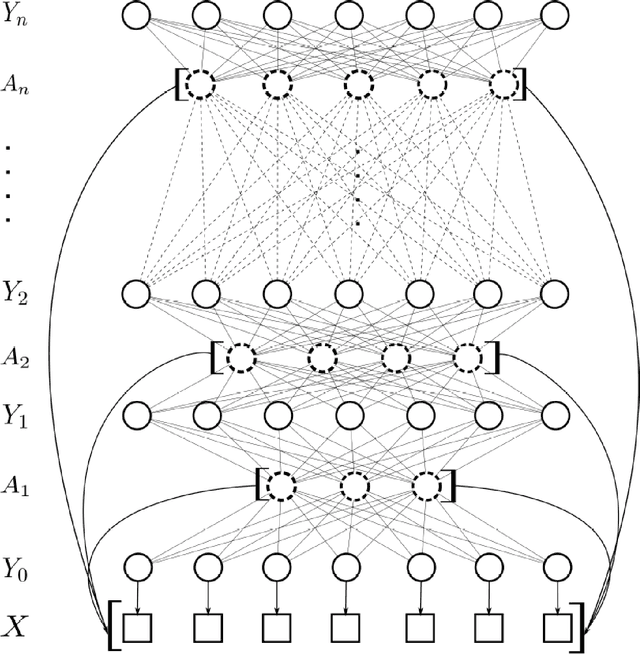
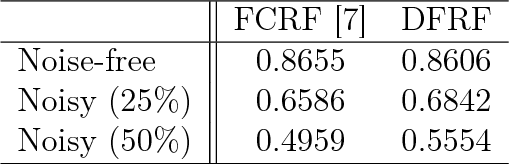

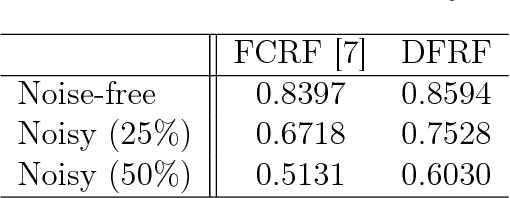
There has been significant interest in the use of fully-connected graphical models and deep-structured graphical models for the purpose of structured inference. However, fully-connected and deep-structured graphical models have been largely explored independently, leaving the unification of these two concepts ripe for exploration. A fundamental challenge with unifying these two types of models is in dealing with computational complexity. In this study, we investigate the feasibility of unifying fully-connected and deep-structured models in a computationally tractable manner for the purpose of structured inference. To accomplish this, we introduce a deep-structured fully-connected random field (DFRF) model that integrates a series of intermediate sparse auto-encoding layers placed between state layers to significantly reduce computational complexity. The problem of image segmentation was used to illustrate the feasibility of using the DFRF for structured inference in a computationally tractable manner. Results in this study show that it is feasible to unify fully-connected and deep-structured models in a computationally tractable manner for solving structured inference problems such as image segmentation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge