A Bridge Between Hyperparameter Optimization and Larning-to-learn
Paper and Code
Feb 04, 2018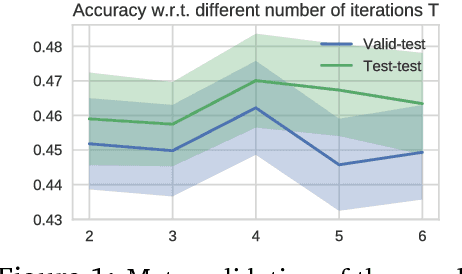
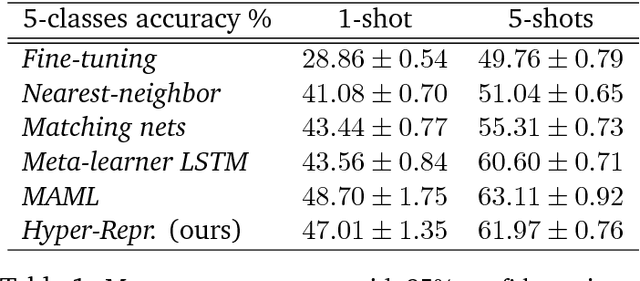
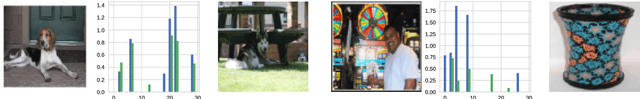
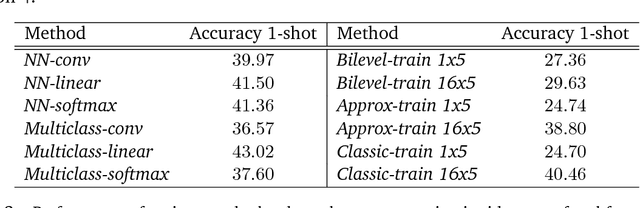
We consider a class of a nested optimization problems involving inner and outer objectives. We observe that by taking into explicit account the optimization dynamics for the inner objective it is possible to derive a general framework that unifies gradient-based hyperparameter optimization and meta-learning (or learning-to-learn). Depending on the specific setting, the variables of the outer objective take either the meaning of hyperparameters in a supervised learning problem or parameters of a meta-learner. We show that some recently proposed methods in the latter setting can be instantiated in our framework and tackled with the same gradient-based algorithms. Finally, we discuss possible design patterns for learning-to-learn and present encouraging preliminary experiments for few-shot learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge