From NLVO to NAO: Reactive Robot Navigation using Velocity and Acceleration Obstacles

This paper introduces a novel approach for robot navigation in challenging dynamic environments. The proposed method builds upon the concept of Velocity Obstacles (VO) that was later extended to Nonlinear Velocity Obstacles (NLVO) to account for obstacles moving along nonlinear trajectories. The NLVO is extended in this paper to Acceleration Obstacles (AO) and Nonlinear Acceleration Obstacles (NAO) that account for velocity and acceleration constraints. Multi-robot navigation is achieved by using the same avoidance algorithm by all robots. At each time step, the trajectories of all robots are predicted based on their current velocity and acceleration to allow the computation of their respective NLVO, AO and NAO. The introduction of AO and NAO allows the generation of safe avoidance maneuvers that account for the robot dynamic constraints better than could be done with the NLVO alone. This paper demonstrates the use of AO and NAO for robot navigation in challenging environments. It is shown that using AO and NAO enables simultaneous real-time collision avoidance while accounting for robot kinematics and a direct consideration of its dynamic constraints. The presented approach enables reactive and efficient navigation, with potential application for autonomous vehicles operating in complex dynamic environments.

Robot Navigation in Dynamic Environments using Acceleration Obstacles

This paper addresses the issue of motion planning in dynamic environments by extending the concept of Velocity Obstacle and Nonlinear Velocity Obstacle to Acceleration Obstacle AO and Nonlinear Acceleration Obstacle NAO. Similarly to VO and NLVO, the AO and NAO represent the set of colliding constant accelerations of the maneuvering robot with obstacles moving along linear and nonlinear trajectories, respectively. Contrary to prior works, we derive analytically the exact boundaries of AO and NAO. To enhance an intuitive understanding of these representations, we first derive the AO in several steps: first extending the VO to the Basic Acceleration Obstacle BAO that consists of the set of constant accelerations of the robot that would collide with an obstacle moving at constant accelerations, while assuming zero initial velocities of the robot and obstacle. This is then extended to the AO while assuming arbitrary initial velocities of the robot and obstacle. And finally, we derive the NAO that in addition to the prior assumptions, accounts for obstacles moving along arbitrary trajectories. The introduction of NAO allows the generation of safe avoidance maneuvers that directly account for the robot's second-order dynamics, with acceleration as its control input. The AO and NAO are demonstrated in several examples of selecting avoidance maneuvers in challenging road traffic. It is shown that the use of NAO drastically reduces the adjustment rate of the maneuvering robot's acceleration while moving in complex road traffic scenarios. The presented approach enables reactive and efficient navigation for multiple robots, with potential application for autonomous vehicles operating in complex dynamic environments.

Autonomous Head-to-Head Racing in the Indy Autonomous Challenge Simulation Race

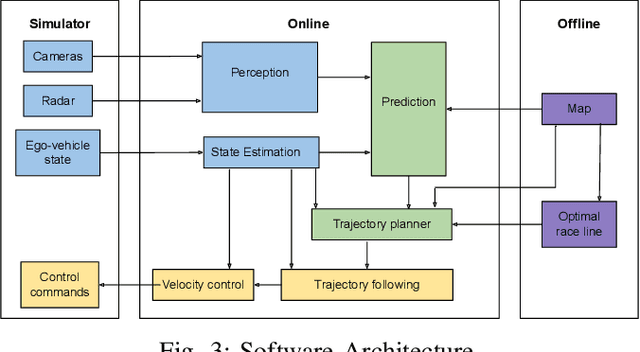
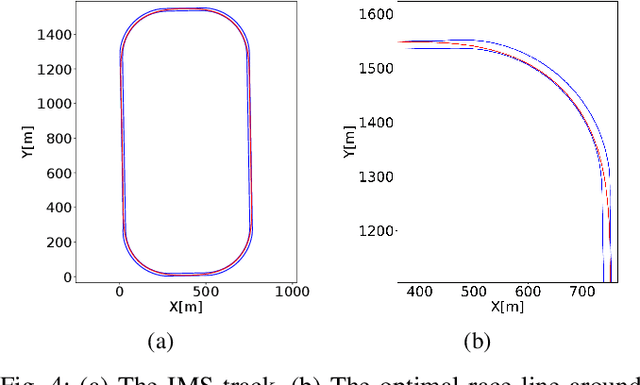
This paper describes Ariel Team's autonomous racing controller for the Indy Autonomous Challenge (IAC) simulation race \cite{INDY}. IAC is the first multi-vehicle autonomous head-to-head competition, reaching speeds of 300 km/h along an oval track, modeled after the Indianapolis Motor Speedway (IMS). Our racing controller attempts to maximize progress along the track while avoiding collisions with opponent vehicles and obeying the race rules. To this end, the racing controller first computes a race line offline. Then, it repeatedly computes online a small set of dynamically feasible maneuver candidates, each tested for collision with the opponent vehicles. Finally, it selects the maneuver that maximizes progress along the track, taking into account the race line. The maneuver candidates, as well as the predicted trajectories of the opponent vehicles, are approximated using a point mass model. Despite the simplicity of this racing controller, it managed to drive competitively and with no collision with any of the opponent vehicles in the IAC final simulation race.

Deep Reinforcement Learning for Time Optimal Velocity Control using Prior Knowledge

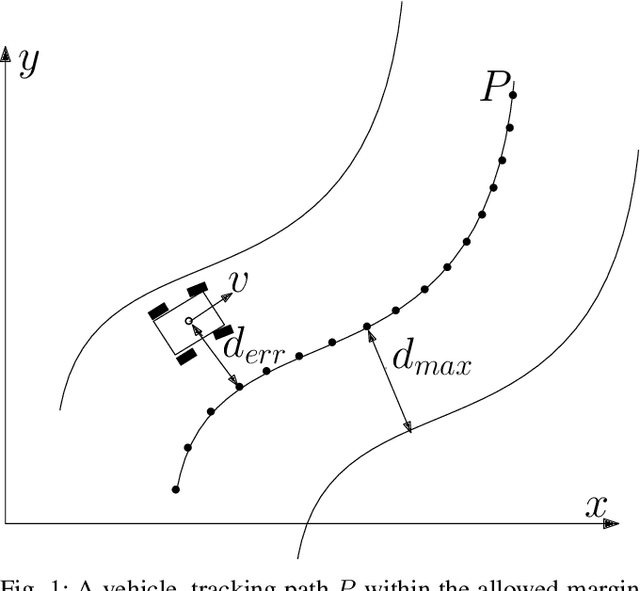
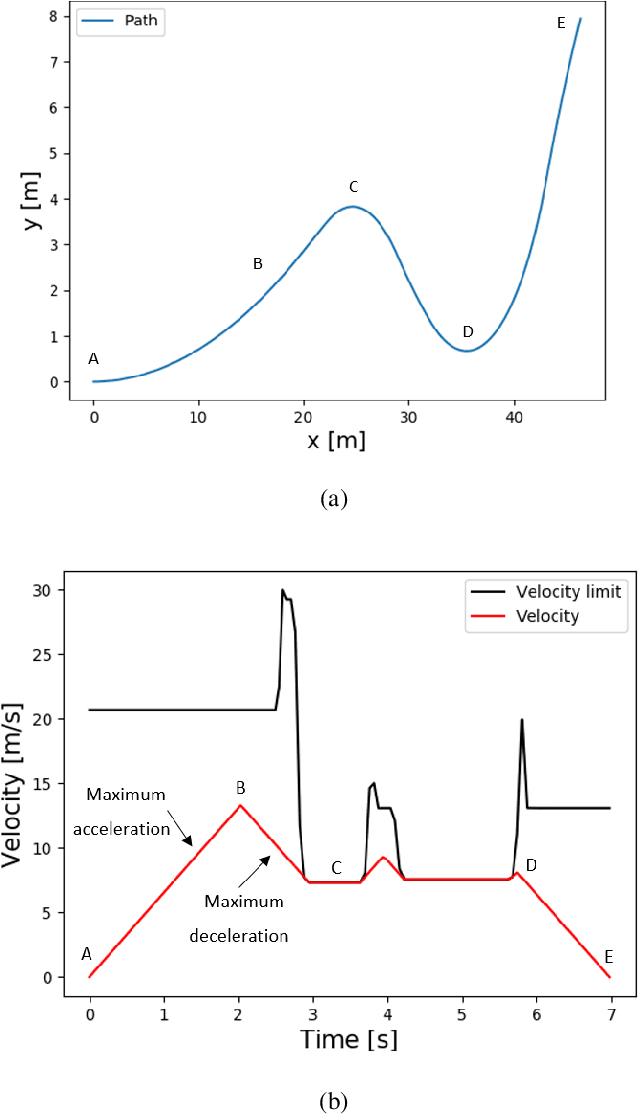
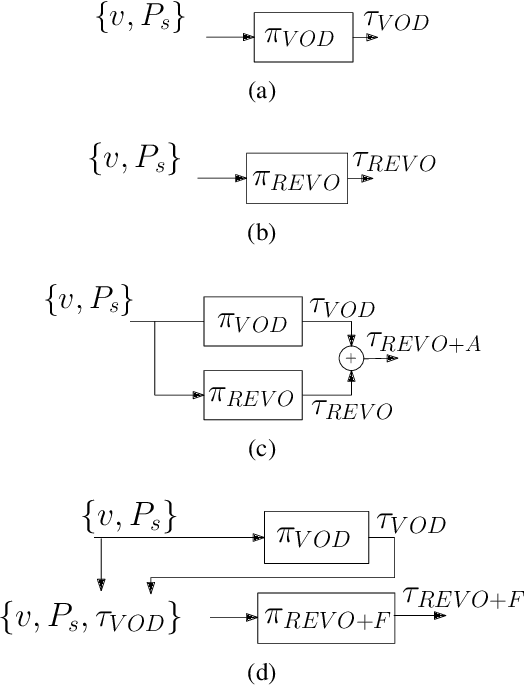
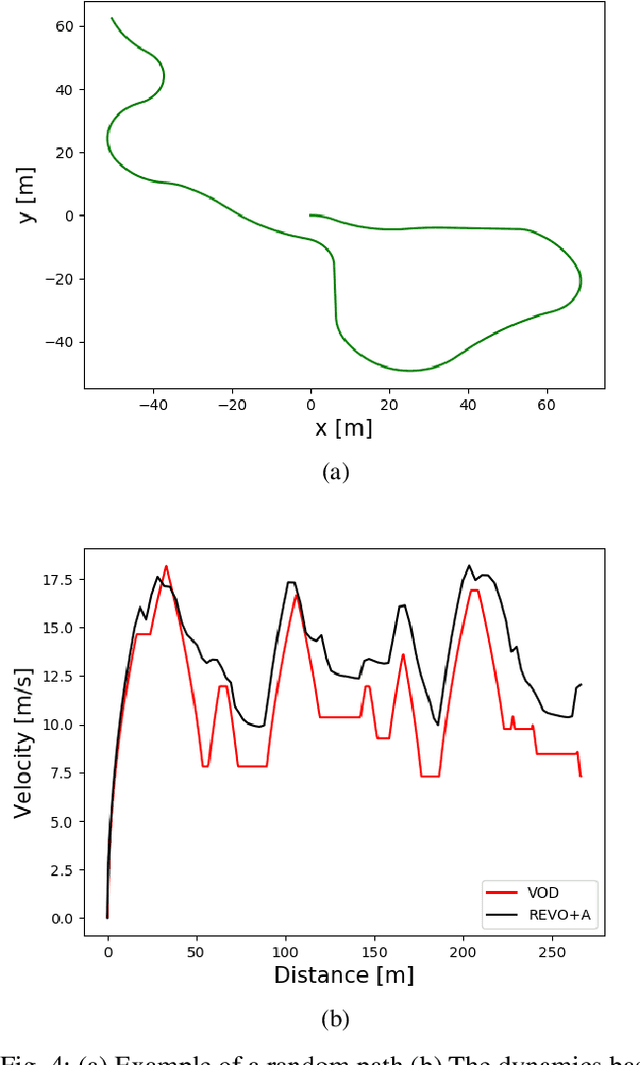
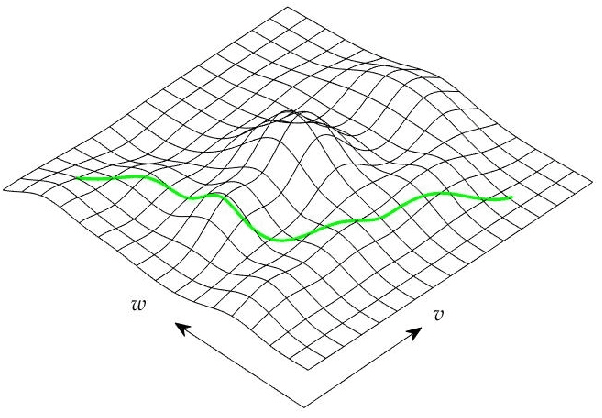
While autonomous navigation has recently gained great interest in the field of reinforcement learning, only a few works in this field have focused on the time optimal velocity control problem, i.e. controlling a vehicle such that it travels at the maximal speed without becoming dynamically unstable. Achieving maximal speed is important in many situations, such as emergency vehicles traveling at high speeds to their destinations, and regular vehicles executing emergency maneuvers to avoid imminent collisions. Time optimal velocity control can be solved numerically using existing methods that are based on optimal control and vehicle dynamics. In this paper, we use deep reinforcement learning to generate the time optimal velocity control. Furthermore, we use the numerical solution to further improve the performance of the reinforcement learner. It is shown that the reinforcement learner outperforms the numerically derived solution, and that the hybrid approach (combining learning with the numerical solution) speeds up the learning process.

Pose Estimation of Vehicles Over Uneven Terrain

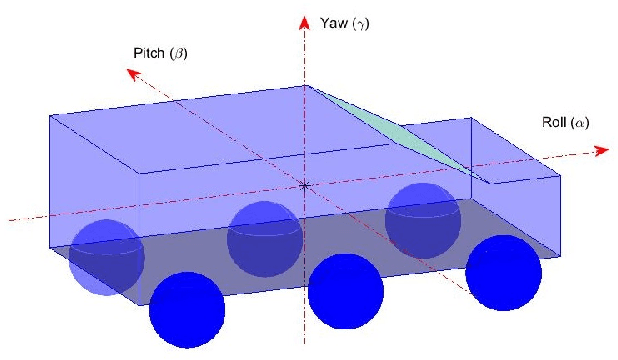
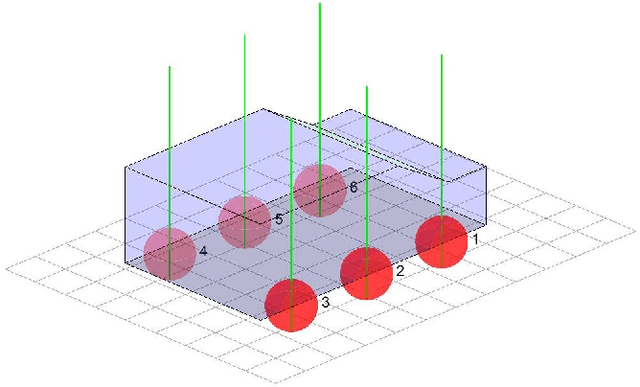
This paper presents a method for pose estimation of off-road vehicles moving over uneven terrain. It determines the contact points between the wheels and the terrain, assuming rigid contacts between an arbitrary number of wheels and ground. The terrain is represented by a 3D points cloud, interpolated by a B-patch to provide a continuous terrain representation. The pose estimation problem is formulated as a rigid body contact problem for a given location of the vehicle's center of mass over the terrain and a given yaw angle. The contact points between the wheels and ground are determined by releasing the vehicle from a given point above the terrain, until the contact forces between the wheels and ground, and the gravitational force, reach equilibrium. The contact forces are calculated using singular value decomposition (SVD) of the deduced contact matrix. The proposed method is computationally efficient, allowing real time computation during motion, as demonstrated in several examples. Accurate pose estimations can be used for motion planning, stability analyses and traversability analyses over uneven terrain.