Feedforward 3D Editing via Text-Steerable Image-to-3D

Recent progress in image-to-3D has opened up immense possibilities for design, AR/VR, and robotics. However, to use AI-generated 3D assets in real applications, a critical requirement is the capability to edit them easily. We present a feedforward method, Steer3D, to add text steerability to image-to-3D models, which enables editing of generated 3D assets with language. Our approach is inspired by ControlNet, which we adapt to image-to-3D generation to enable text steering directly in a forward pass. We build a scalable data engine for automatic data generation, and develop a two-stage training recipe based on flow-matching training and Direct Preference Optimization (DPO). Compared to competing methods, Steer3D more faithfully follows the language instruction and maintains better consistency with the original 3D asset, while being 2.4x to 28.5x faster. Steer3D demonstrates that it is possible to add a new modality (text) to steer the generation of pretrained image-to-3D generative models with 100k data. Project website: https://glab-caltech.github.io/steer3d/

Find Any Part in 3D

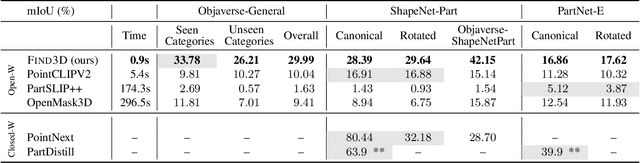
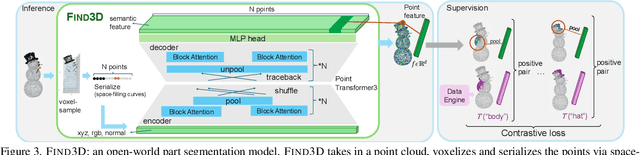
We study open-world part segmentation in 3D: segmenting any part in any object based on any text query. Prior methods are limited in object categories and part vocabularies. Recent advances in AI have demonstrated effective open-world recognition capabilities in 2D. Inspired by this progress, we propose an open-world, direct-prediction model for 3D part segmentation that can be applied zero-shot to any object. Our approach, called Find3D, trains a general-category point embedding model on large-scale 3D assets from the internet without any human annotation. It combines a data engine, powered by foundation models for annotating data, with a contrastive training method. We achieve strong performance and generalization across multiple datasets, with up to a 3x improvement in mIoU over the next best method. Our model is 6x to over 300x faster than existing baselines. To encourage research in general-category open-world 3D part segmentation, we also release a benchmark for general objects and parts. Project website: https://ziqi-ma.github.io/find3dsite/

Calibrated Uncertainty Quantification for Operator Learning via Conformal Prediction

Operator learning has been increasingly adopted in scientific and engineering applications, many of which require calibrated uncertainty quantification. Since the output of operator learning is a continuous function, quantifying uncertainty simultaneously at all points in the domain is challenging. Current methods consider calibration at a single point or over one scalar function or make strong assumptions such as Gaussianity. We propose a risk-controlling quantile neural operator, a distribution-free, finite-sample functional calibration conformal prediction method. We provide a theoretical calibration guarantee on the coverage rate, defined as the expected percentage of points on the function domain whose true value lies within the predicted uncertainty ball. Empirical results on a 2D Darcy flow and a 3D car surface pressure prediction task validate our theoretical results, demonstrating calibrated coverage and efficient uncertainty bands outperforming baseline methods. In particular, on the 3D problem, our method is the only one that meets the target calibration percentage (percentage of test samples for which the uncertainty estimates are calibrated) of 98%.