Ziliang Samuel Zhong
Bridging Domains with Approximately Shared Features
Mar 11, 2024Abstract:Multi-source domain adaptation aims to reduce performance degradation when applying machine learning models to unseen domains. A fundamental challenge is devising the optimal strategy for feature selection. Existing literature is somewhat paradoxical: some advocate for learning invariant features from source domains, while others favor more diverse features. To address the challenge, we propose a statistical framework that distinguishes the utilities of features based on the variance of their correlation to label $y$ across domains. Under our framework, we design and analyze a learning procedure consisting of learning approximately shared feature representation from source tasks and fine-tuning it on the target task. Our theoretical analysis necessitates the importance of learning approximately shared features instead of only the strictly invariant features and yields an improved population risk compared to previous results on both source and target tasks, thus partly resolving the paradox mentioned above. Inspired by our theory, we proposed a more practical way to isolate the content (invariant+approximately shared) from environmental features and further consolidate our theoretical findings.
Improved theoretical guarantee for rank aggregation via spectral method
Sep 10, 2023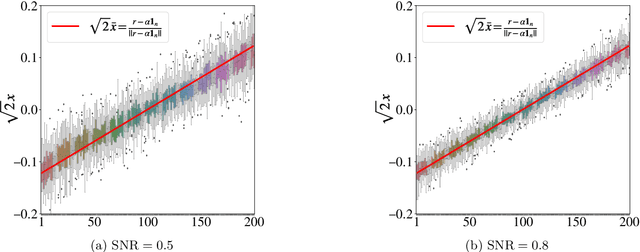
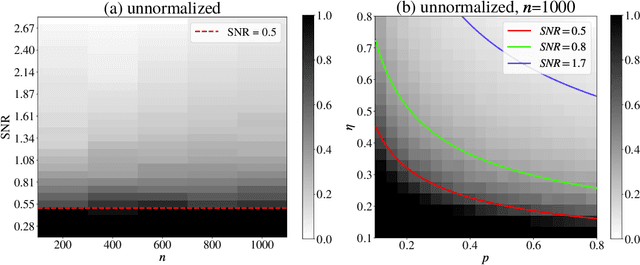
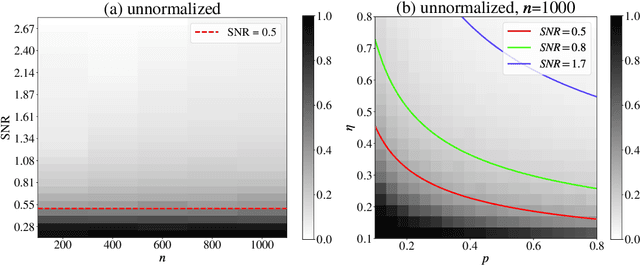
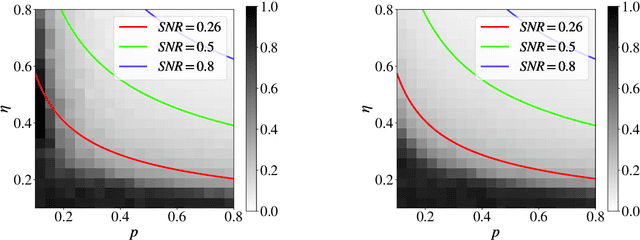
Abstract:Given pairwise comparisons between multiple items, how to rank them so that the ranking matches the observations? This problem, known as rank aggregation, has found many applications in sports, recommendation systems, and other web applications. As it is generally NP-hard to find a global ranking that minimizes the mismatch (known as the Kemeny optimization), we focus on the Erd\"os-R\'enyi outliers (ERO) model for this ranking problem. Here, each pairwise comparison is a corrupted copy of the true score difference. We investigate spectral ranking algorithms that are based on unnormalized and normalized data matrices. The key is to understand their performance in recovering the underlying scores of each item from the observed data. This reduces to deriving an entry-wise perturbation error bound between the top eigenvectors of the unnormalized/normalized data matrix and its population counterpart. By using the leave-one-out technique, we provide a sharper $\ell_{\infty}$-norm perturbation bound of the eigenvectors and also derive an error bound on the maximum displacement for each item, with only $\Omega(n\log n)$ samples. Our theoretical analysis improves upon the state-of-the-art results in terms of sample complexity, and our numerical experiments confirm these theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge