Integrating Generative and Physics-Based Models for Ptychographic Imaging with Uncertainty Quantification

Ptychography is a scanning coherent diffractive imaging technique that enables imaging nanometer-scale features in extended samples. One main challenge is that widely used iterative image reconstruction methods often require significant amount of overlap between adjacent scan locations, leading to large data volumes and prolonged acquisition times. To address this key limitation, this paper proposes a Bayesian inversion method for ptychography that performs effectively even with less overlap between neighboring scan locations. Furthermore, the proposed method can quantify the inherent uncertainty on the ptychographic object, which is created by the ill-posed nature of the ptychographic inverse problem. At a high level, the proposed method first utilizes a deep generative model to learn the prior distribution of the object and then generates samples from the posterior distribution of the object by using a Markov Chain Monte Carlo algorithm. Our results from simulated ptychography experiments show that the proposed framework can consistently outperform a widely used iterative reconstruction algorithm in cases of reduced overlap. Moreover, the proposed framework can provide uncertainty estimates that closely correlate with the true error, which is not available in practice. The project website is available here.

Physics-Inspired Unsupervised Classification for Region of Interest in X-Ray Ptychography

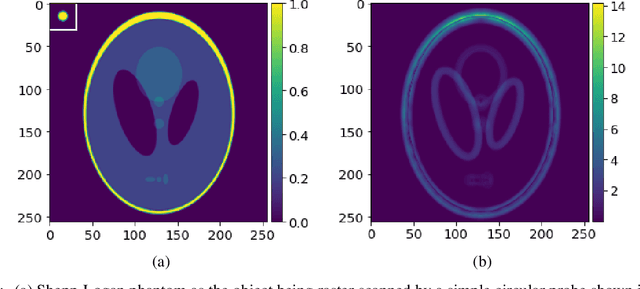
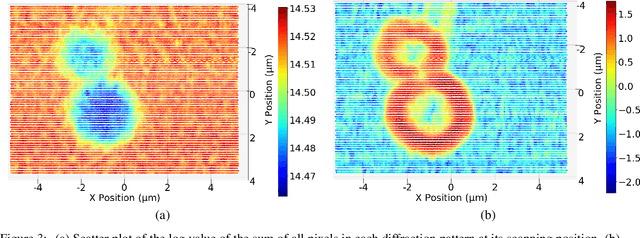
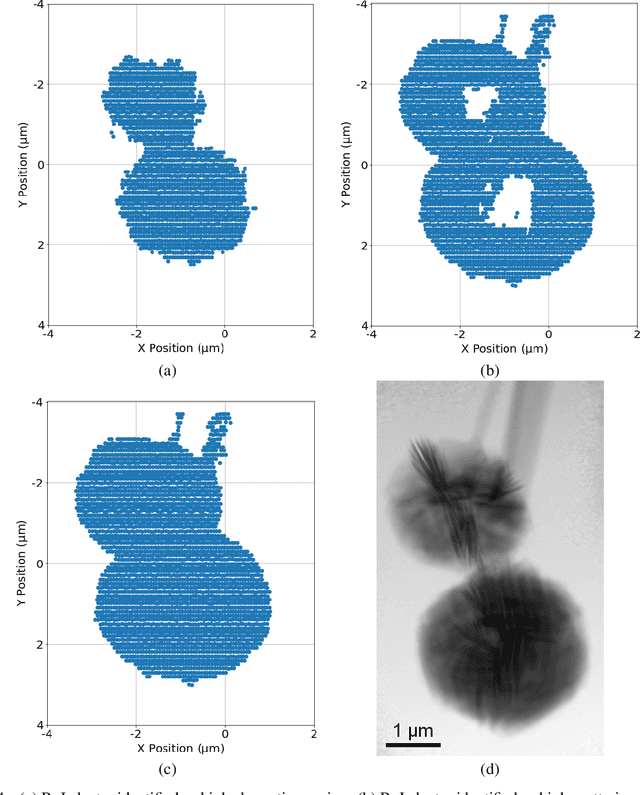
X-ray ptychography allows for large fields to be imaged at high resolution at the cost of additional computational expense due to the large volume of data. Given limited information regarding the object, the acquired data often has an excessive amount of information that is outside the region of interest (RoI). In this work we propose a physics-inspired unsupervised learning algorithm to identify the RoI of an object using only diffraction patterns from a ptychography dataset before committing computational resources to reconstruction. Obtained diffraction patterns that are automatically identified as not within the RoI are filtered out, allowing efficient reconstruction by focusing only on important data within the RoI while preserving image quality.

Uncertainty quantification for ptychography using normalizing flows

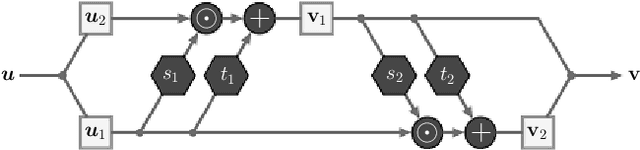
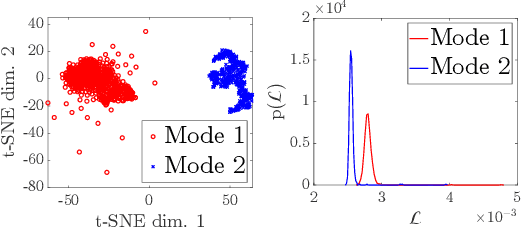
Ptychography, as an essential tool for high-resolution and nondestructive material characterization, presents a challenging large-scale nonlinear and non-convex inverse problem; however, its intrinsic photon statistics create clear opportunities for statistical-based deep learning approaches to tackle these challenges, which has been underexplored. In this work, we explore normalizing flows to obtain a surrogate for the high-dimensional posterior, which also enables the characterization of the uncertainty associated with the reconstruction: an extremely desirable capability when judging the reconstruction quality in the absence of ground truth, spotting spurious artifacts and guiding future experiments using the returned uncertainty patterns. We demonstrate the performance of the proposed method on a synthetic sample with added noise and in various physical experimental settings.

Gaussian Process for Tomography

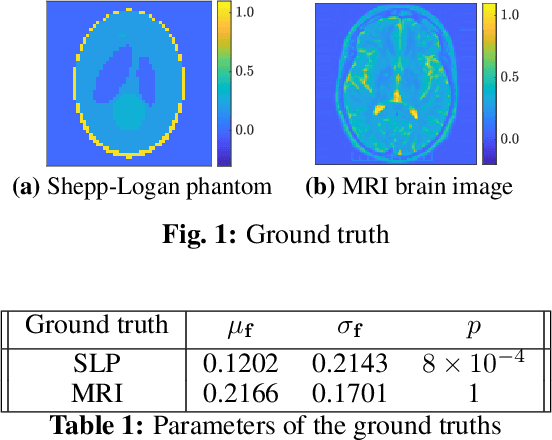
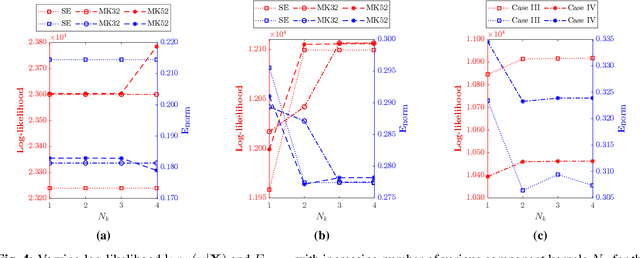
Tomographic reconstruction, despite its revolutionary impact on a wide range of applications, suffers from its ill-posed nature in that there is no unique solution because of limited and noisy measurements. Traditional optimization-based reconstruction relies on regularization to address this issue; however, it faces its own challenge because the type of regularizer and choice of regularization parameter are a critical but difficult decision. Moreover, traditional reconstruction yields point estimates for the reconstruction with no further indication of the quality of the solution. In this work we address these challenges by exploring Gaussian processes (GPs). Our proposed GP approach yields not only the reconstructed object through the posterior mean but also a quantification of the solution uncertainties through the posterior covariance. Furthermore, we explore the flexibility of the GP framework to provide a robust model of the information across various length scales in the object, as well as the complex noise in the measurements. We illustrate the proposed approach on both synthetic and real tomography images and show its unique capability of uncertainty quantification in the presence of various types of noise, as well as reconstruction comparison with existing methods.