OS-net: Orbitally Stable Neural Networks

We introduce OS-net (Orbitally Stable neural NETworks), a new family of neural network architectures specifically designed for periodic dynamical data. OS-net is a special case of Neural Ordinary Differential Equations (NODEs) and takes full advantage of the adjoint method based backpropagation method. Utilizing ODE theory, we derive conditions on the network weights to ensure stability of the resulting dynamics. We demonstrate the efficacy of our approach by applying OS-net to discover the dynamics underlying the R\"{o}ssler and Sprott's systems, two dynamical systems known for their period doubling attractors and chaotic behavior.

Targeted Adaptive Design

Modern advanced manufacturing and advanced materials design often require searches of relatively high-dimensional process control parameter spaces for settings that result in optimal structure, property, and performance parameters. The mapping from the former to the latter must be determined from noisy experiments or from expensive simulations. We abstract this problem to a mathematical framework in which an unknown function from a control space to a design space must be ascertained by means of expensive noisy measurements, which locate optimal control settings generating desired design features within specified tolerances, with quantified uncertainty. We describe targeted adaptive design (TAD), a new algorithm that performs this optimal sampling task. TAD creates a Gaussian process surrogate model of the unknown mapping at each iterative stage, proposing a new batch of control settings to sample experimentally and optimizing the updated log-predictive likelihood of the target design. TAD either stops upon locating a solution with uncertainties that fit inside the tolerance box or uses a measure of expected future information to determine that the search space has been exhausted with no solution. TAD thus embodies the exploration-exploitation tension in a manner that recalls, but is essentially different from, Bayesian optimization and optimal experimental design.

A Deep Learning Approach to Probabilistic Forecasting of Weather

We discuss an approach to probabilistic forecasting based on two chained machine-learning steps: a dimensional reduction step that learns a reduction map of predictor information to a low-dimensional space in a manner designed to preserve information about forecast quantities; and a density estimation step that uses the probabilistic machine learning technique of normalizing flows to compute the joint probability density of reduced predictors and forecast quantities. This joint density is then renormalized to produce the conditional forecast distribution. In this method, probabilistic calibration testing plays the role of a regularization procedure, preventing overfitting in the second step, while effective dimensional reduction from the first step is the source of forecast sharpness. We verify the method using a 22-year 1-hour cadence time series of Weather Research and Forecasting (WRF) simulation data of surface wind on a grid.

Gaussian Process for Tomography

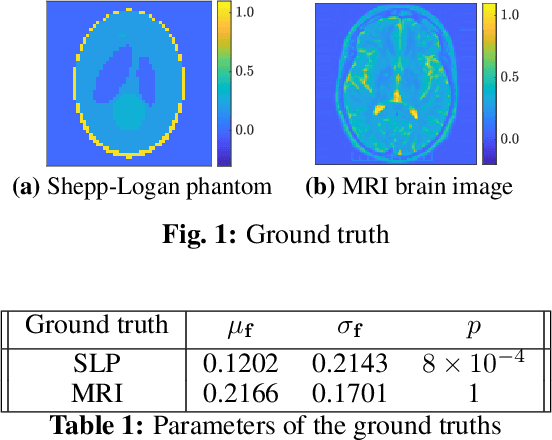
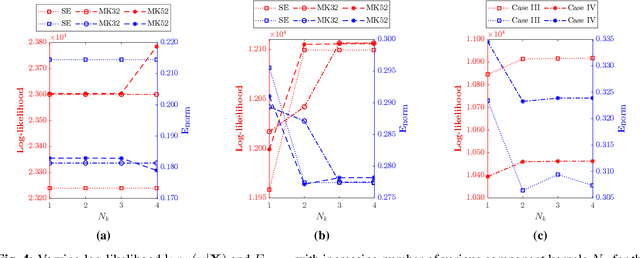
Tomographic reconstruction, despite its revolutionary impact on a wide range of applications, suffers from its ill-posed nature in that there is no unique solution because of limited and noisy measurements. Traditional optimization-based reconstruction relies on regularization to address this issue; however, it faces its own challenge because the type of regularizer and choice of regularization parameter are a critical but difficult decision. Moreover, traditional reconstruction yields point estimates for the reconstruction with no further indication of the quality of the solution. In this work we address these challenges by exploring Gaussian processes (GPs). Our proposed GP approach yields not only the reconstructed object through the posterior mean but also a quantification of the solution uncertainties through the posterior covariance. Furthermore, we explore the flexibility of the GP framework to provide a robust model of the information across various length scales in the object, as well as the complex noise in the measurements. We illustrate the proposed approach on both synthetic and real tomography images and show its unique capability of uncertainty quantification in the presence of various types of noise, as well as reconstruction comparison with existing methods.