Distribution Learning with Valid Outputs Beyond the Worst-Case

Generative models at times produce "invalid" outputs, such as images with generation artifacts and unnatural sounds. Validity-constrained distribution learning attempts to address this problem by requiring that the learned distribution have a provably small fraction of its mass in invalid parts of space -- something which standard loss minimization does not always ensure. To this end, a learner in this model can guide the learning via "validity queries", which allow it to ascertain the validity of individual examples. Prior work on this problem takes a worst-case stance, showing that proper learning requires an exponential number of validity queries, and demonstrating an improper algorithm which -- while generating guarantees in a wide-range of settings -- makes an atypical polynomial number of validity queries. In this work, we take a first step towards characterizing regimes where guaranteeing validity is easier than in the worst-case. We show that when the data distribution lies in the model class and the log-loss is minimized, the number of samples required to ensure validity has a weak dependence on the validity requirement. Additionally, we show that when the validity region belongs to a VC-class, a limited number of validity queries are often sufficient.

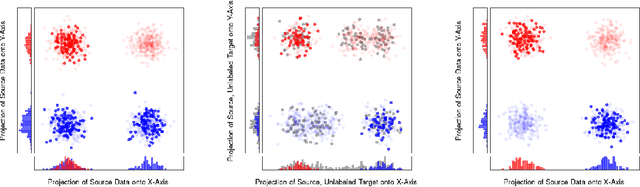
Beyond Discrepancy: A Closer Look at the Theory of Distribution Shift

Many machine learning models appear to deploy effortlessly under distribution shift, and perform well on a target distribution that is considerably different from the training distribution. Yet, learning theory of distribution shift bounds performance on the target distribution as a function of the discrepancy between the source and target, rarely guaranteeing high target accuracy. Motivated by this gap, this work takes a closer look at the theory of distribution shift for a classifier from a source to a target distribution. Instead of relying on the discrepancy, we adopt an Invariant-Risk-Minimization (IRM)-like assumption connecting the distributions, and characterize conditions under which data from a source distribution is sufficient for accurate classification of the target. When these conditions are not met, we show when only unlabeled data from the target is sufficient, and when labeled target data is needed. In all cases, we provide rigorous theoretical guarantees in the large sample regime.

Agnostic Multi-Group Active Learning

Inspired by the problem of improving classification accuracy on rare or hard subsets of a population, there has been recent interest in models of learning where the goal is to generalize to a collection of distributions, each representing a ``group''. We consider a variant of this problem from the perspective of active learning, where the learner is endowed with the power to decide which examples are labeled from each distribution in the collection, and the goal is to minimize the number of label queries while maintaining PAC-learning guarantees. Our main challenge is that standard active learning techniques such as disagreement-based active learning do not directly apply to the multi-group learning objective. We modify existing algorithms to provide a consistent active learning algorithm for an agnostic formulation of multi-group learning, which given a collection of $G$ distributions and a hypothesis class $\mathcal{H}$ with VC-dimension $d$, outputs an $\epsilon$-optimal hypothesis using $\tilde{O}\left( (\nu^2/\epsilon^2+1) G d \theta_{\mathcal{G}}^2 \log^2(1/\epsilon) + G\log(1/\epsilon)/\epsilon^2 \right)$ label queries, where $\theta_{\mathcal{G}}$ is the worst-case disagreement coefficient over the collection. Roughly speaking, this guarantee improves upon the label complexity of standard multi-group learning in regimes where disagreement-based active learning algorithms may be expected to succeed, and the number of groups is not too large. We also consider the special case where each distribution in the collection is individually realizable with respect to $\mathcal{H}$, and demonstrate $\tilde{O}\left( G d \theta_{\mathcal{G}} \log(1/\epsilon) \right)$ label queries are sufficient for learning in this case. We further give an approximation result for the full agnostic case inspired by the group realizable strategy.

A Two-Stage Active Learning Algorithm for $k$-Nearest Neighbors

We introduce a simple and intuitive two-stage active learning algorithm for the training of $k$-nearest neighbors classifiers. We provide consistency guarantees for a modified $k$-nearest neighbors classifier trained on samples acquired via our scheme, and show that when the conditional probability function $\mathbb{P}(Y=y|X=x)$ is sufficiently smooth and the Tsybakov noise condition holds, our actively trained classifiers converge to the Bayes optimal classifier at a faster asymptotic rate than passively trained $k$-nearest neighbor classifiers.

A Deep Learning Approach to Probabilistic Forecasting of Weather

We discuss an approach to probabilistic forecasting based on two chained machine-learning steps: a dimensional reduction step that learns a reduction map of predictor information to a low-dimensional space in a manner designed to preserve information about forecast quantities; and a density estimation step that uses the probabilistic machine learning technique of normalizing flows to compute the joint probability density of reduced predictors and forecast quantities. This joint density is then renormalized to produce the conditional forecast distribution. In this method, probabilistic calibration testing plays the role of a regularization procedure, preventing overfitting in the second step, while effective dimensional reduction from the first step is the source of forecast sharpness. We verify the method using a 22-year 1-hour cadence time series of Weather Research and Forecasting (WRF) simulation data of surface wind on a grid.