Fully Robust Federated Submodel Learning in a Distributed Storage System

We consider the federated submodel learning (FSL) problem in a distributed storage system. In the FSL framework, the full learning model at the server side is divided into multiple submodels such that each selected client needs to download only the required submodel(s) and upload the corresponding update(s) in accordance with its local training data. The server comprises multiple independent databases and the full model is stored across these databases. An eavesdropper passively observes all the storage and listens to all the communicated data, of its controlled databases, to gain knowledge about the remote client data and the submodel information. In addition, a subset of databases may fail, negatively affecting the FSL process, as FSL process may take a non-negligible amount of time for large models. To resolve these two issues together (i.e., security and database repair), we propose a novel coding mechanism coined ramp secure regenerating coding (RSRC), to store the full model in a distributed manner. Using our new RSRC method, the eavesdropper is permitted to learn a controllable amount of submodel information for the sake of reducing the communication and storage costs. Further, during the database repair process, in the construction of the replacement database, the submodels to be updated are stored in the form of their latest version from updating clients, while the remaining submodels are obtained from the previous version in other databases through routing clients. Our new RSRC-based distributed FSL approach is constructed on top of our earlier two-database FSL scheme which uses private set union (PSU). A complete one-round FSL process consists of FSL-PSU phase, FSL-write phase and additional auxiliary phases. Our proposed FSL scheme is also robust against database drop-outs, client drop-outs, client late-arrivals and an active adversary controlling databases.

Private Information Retrieval and Its Applications: An Introduction, Open Problems, Future Directions

Private information retrieval (PIR) is a privacy setting that allows a user to download a required message from a set of messages stored in a system of databases without revealing the index of the required message to the databases. PIR was introduced under computational privacy guarantees, and is recently re-formulated to provide information-theoretic guarantees, resulting in \emph{information theoretic privacy}. Subsequently, many important variants of the basic PIR problem have been studied focusing on fundamental performance limits as well as achievable schemes. More recently, a variety of conceptual extensions of PIR have been introduced, such as, private set intersection (PSI), private set union (PSU), and private read-update-write (PRUW). Some of these extensions are mainly intended to solve the privacy issues that arise in distributed learning applications due to the extensive dependency of machine learning on users' private data. In this article, we first provide an introduction to basic PIR with examples, followed by a brief description of its immediate variants. We then provide a detailed discussion on the conceptual extensions of PIR, along with potential research directions.

Private Federated Submodel Learning via Private Set Union

We consider the federated submodel learning (FSL) problem and propose an approach where clients are able to update the central model information theoretically privately. Our approach is based on private set union (PSU), which is further based on multi-message symmetric private information retrieval (MM-SPIR). The server has two non-colluding databases which keep the model in a replicated manner. With our scheme, the server does not get to learn anything further than the subset of submodels updated by the clients: the server does not get to know which client updated which submodel(s), or anything about the local client data. In comparison to the state-of-the-art private FSL schemes of Jia-Jafar and Vithana-Ulukus, our scheme does not require noisy storage of the model at the databases; and in comparison to the secure aggregation scheme of Zhao-Sun, our scheme does not require pre-distribution of client-side common randomness, instead, our scheme creates the required client-side common randomness via random SPIR and one-time pads. The protocol starts with a common randomness generation (CRG) phase where the two databases establish common randomness at the client-side using RSPIR and one-time pads (this phase is called FSL-CRG). Next, the clients utilize the established client-side common randomness to have the server determine privately the union of indices of submodels to be updated collectively by the clients (this phase is called FSL-PSU). Then, the two databases broadcast the current versions of the submodels in the set union to clients. The clients update the submodels based on their local training data. Finally, the clients use a variation of FSL-PSU to write the updates back to the databases privately (this phase is called FSL-write). Our proposed private FSL scheme is robust against client drop-outs, client late-arrivals, and database drop-outs.

Digital Blind Box: Random Symmetric Private Information Retrieval

We introduce the problem of random symmetric private information retrieval (RSPIR). In canonical PIR, a user downloads a message out of $K$ messages from $N$ non-colluding and replicated databases in such a way that no database can know which message the user has downloaded (user privacy). In SPIR, the privacy is symmetric, in that, not only that the databases cannot know which message the user has downloaded, the user itself cannot learn anything further than the particular message it has downloaded (database privacy). In RSPIR, different from SPIR, the user does not have an input to the databases, i.e., the user does not pick a specific message to download, instead is content with any one of the messages. In RSPIR, the databases need to send symbols to the user in such a way that the user is guaranteed to download a message correctly (random reliability), the databases do not know which message the user has received (user privacy), and the user does not learn anything further than the one message it has received (database privacy). This is the digital version of a blind box, also known as gachapon, which implements the above specified setting with physical objects for entertainment. This is also the blind version of $1$-out-of-$K$ oblivious transfer (OT), an important cryptographic primitive. We study the information-theoretic capacity of RSPIR for the case of $N=2$ databases. We determine its exact capacity for the cases of $K = 2, 3, 4$ messages. While we provide a general achievable scheme that is applicable to any number of messages, the capacity for $K\geq 5$ remains open.

Communication Cost of Two-Database Symmetric Private Information Retrieval: A Conditional Disclosure of Multiple Secrets Perspective

We consider the total (upload plus download) communication cost of two-database symmetric private information retrieval (SPIR) through its relationship to conditional disclosure of secrets (CDS). In SPIR, a user wishes to retrieve a message out of $K$ messages from $N$ non-colluding and replicated databases without learning anything beyond the retrieved message, while no individual database learns the retrieved message index. In CDS, two parties each holding an individual input and sharing a common secret wish to disclose this secret to an external party in an efficient manner if and only if their inputs satisfy a public deterministic function. As a natural extension of CDS, we introduce conditional disclosure of multiple secrets (CDMS) where two parties share multiple i.i.d.~common secrets rather than a single common secret as in CDS. We show that a special configuration of CDMS is equivalent to two-database SPIR. Inspired by this equivalence, we design download cost efficient SPIR schemes using bipartite graph representation of CDS and CDMS, and determine the exact minimum total communication cost of $N=2$ database SPIR for $K=3$ messages.

Symmetric Private Information Retrieval with User-Side Common Randomness

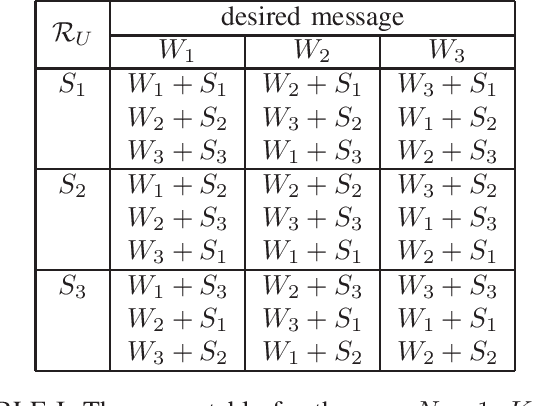
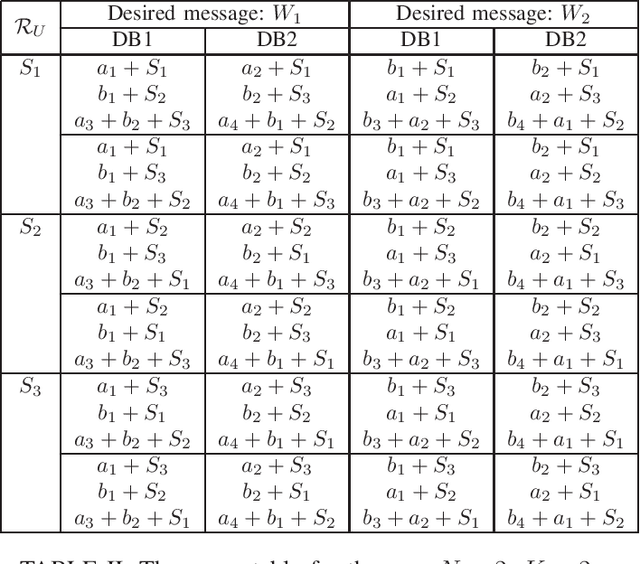
We consider the problem of symmetric private information retrieval (SPIR) with user-side common randomness. In SPIR, a user retrieves a message out of $K$ messages from $N$ non-colluding and replicated databases in such a way that no single database knows the retrieved message index (user privacy), and the user gets to know nothing further than the retrieved message (database privacy). SPIR has a capacity smaller than the PIR capacity which requires only user privacy, is infeasible in the case of a single database, and requires shared common randomness among the databases. We introduce a new variant of SPIR where the user is provided with a random subset of the shared database common randomness, which is unknown to the databases. We determine the exact capacity region of the triple $(d, \rho_S, \rho_U)$, where $d$ is the download cost, $\rho_S$ is the amount of shared database (server) common randomness, and $\rho_U$ is the amount of available user-side common randomness. We show that with a suitable amount of $\rho_U$, this new SPIR achieves the capacity of conventional PIR. As a corollary, single-database SPIR becomes feasible. Further, the presence of user-side $\rho_U$ reduces the amount of required server-side $\rho_S$.