Symmetric Private Information Retrieval with User-Side Common Randomness
Paper and Code
May 12, 2021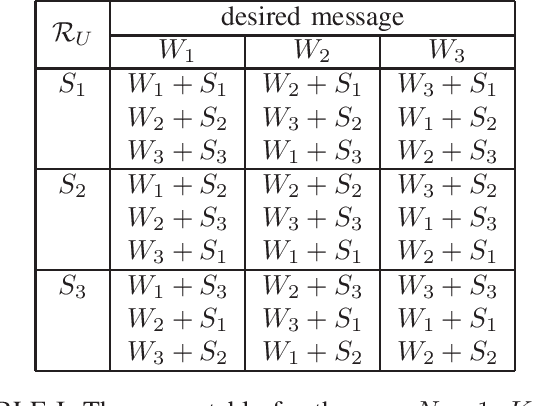
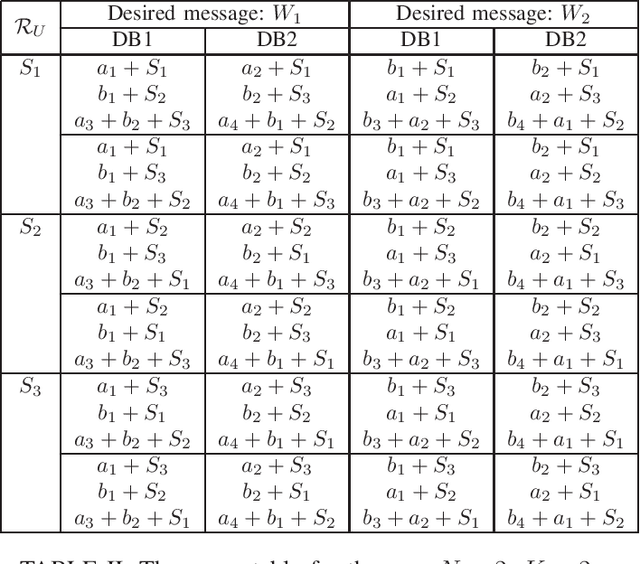
We consider the problem of symmetric private information retrieval (SPIR) with user-side common randomness. In SPIR, a user retrieves a message out of $K$ messages from $N$ non-colluding and replicated databases in such a way that no single database knows the retrieved message index (user privacy), and the user gets to know nothing further than the retrieved message (database privacy). SPIR has a capacity smaller than the PIR capacity which requires only user privacy, is infeasible in the case of a single database, and requires shared common randomness among the databases. We introduce a new variant of SPIR where the user is provided with a random subset of the shared database common randomness, which is unknown to the databases. We determine the exact capacity region of the triple $(d, \rho_S, \rho_U)$, where $d$ is the download cost, $\rho_S$ is the amount of shared database (server) common randomness, and $\rho_U$ is the amount of available user-side common randomness. We show that with a suitable amount of $\rho_U$, this new SPIR achieves the capacity of conventional PIR. As a corollary, single-database SPIR becomes feasible. Further, the presence of user-side $\rho_U$ reduces the amount of required server-side $\rho_S$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge