Zhongzheng Xiong
Adversarially Robust Distributed Count Tracking via Partial Differential Privacy
Nov 01, 2023Abstract:We study the distributed tracking model, also known as distributed functional monitoring. This model involves $k$ sites each receiving a stream of items and communicating with the central server. The server's task is to track a function of all items received thus far continuously, with minimum communication cost. For count tracking, it is known that there is a $\sqrt{k}$ gap in communication between deterministic and randomized algorithms. However, existing randomized algorithms assume an "oblivious adversary" who constructs the entire input streams before the algorithm starts. Here we consider adaptive adversaries who can choose new items based on previous answers from the algorithm. Deterministic algorithms are trivially robust to adaptive adversaries, while randomized ones may not. Therefore, we investigate whether the $\sqrt{k}$ advantage of randomized algorithms is from randomness itself or the oblivious adversary assumption. We provide an affirmative answer to this question by giving a robust algorithm with optimal communication. Existing robustification techniques do not yield optimal bounds due to the inherent challenges of the distributed nature of the problem. To address this, we extend the differential privacy framework by introducing "partial differential privacy" and proving a new generalization theorem. This theorem may have broader applications beyond robust count tracking, making it of independent interest.
Compressive Privatization: Sparse Distribution Estimation under Locally Differentially Privacy
Dec 03, 2020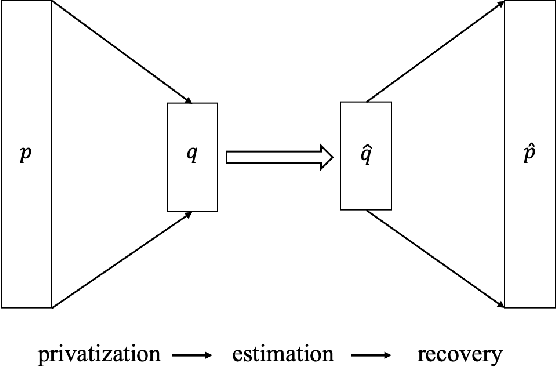



Abstract:We consider the problem of discrete distribution estimation under locally differential privacy. Distribution estimation is one of the most fundamental estimation problems, which is widely studied in both non-private and private settings. In the local model, private mechanisms with provably optimal sample complexity are known. However, they are optimal only in the worst-case sense; their sample complexity is proportional to the size of the entire universe, which could be huge in practice (e.g., all IP addresses). We show that as long as the target distribution is sparse or approximately sparse (e.g., highly skewed), the number of samples needed could be significantly reduced. The sample complexity of our new mechanism is characterized by the sparsity of the target distribution and only weakly depends on the size the universe. Our mechanism does privatization and dimensionality reduction simultaneously, and the sample complexity will only depend on the reduced dimensionality. The original distribution is then recovered using tools from compressive sensing. To complement our theoretical results, we conduct experimental studies, the results of which clearly demonstrate the advantages of our method and confirm our theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge