Compressive Privatization: Sparse Distribution Estimation under Locally Differentially Privacy
Paper and Code
Dec 03, 2020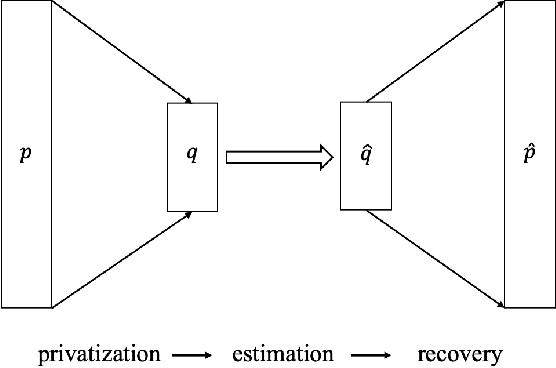



We consider the problem of discrete distribution estimation under locally differential privacy. Distribution estimation is one of the most fundamental estimation problems, which is widely studied in both non-private and private settings. In the local model, private mechanisms with provably optimal sample complexity are known. However, they are optimal only in the worst-case sense; their sample complexity is proportional to the size of the entire universe, which could be huge in practice (e.g., all IP addresses). We show that as long as the target distribution is sparse or approximately sparse (e.g., highly skewed), the number of samples needed could be significantly reduced. The sample complexity of our new mechanism is characterized by the sparsity of the target distribution and only weakly depends on the size the universe. Our mechanism does privatization and dimensionality reduction simultaneously, and the sample complexity will only depend on the reduced dimensionality. The original distribution is then recovered using tools from compressive sensing. To complement our theoretical results, we conduct experimental studies, the results of which clearly demonstrate the advantages of our method and confirm our theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge