Identifying the Hierarchical Emotional Areas in the Human Brain Through Information Fusion

The brain basis of emotion has consistently received widespread attention, attracting a large number of studies to explore this cutting-edge topic. However, the methods employed in these studies typically only model the pairwise relationship between two brain regions, while neglecting the interactions and information fusion among multiple brain regions$\unicode{x2014}$one of the key ideas of the psychological constructionist hypothesis. To overcome the limitations of traditional methods, this study provides an in-depth theoretical analysis of how to maximize interactions and information fusion among brain regions. Building on the results of this analysis, we propose to identify the hierarchical emotional areas in the human brain through multi-source information fusion and graph machine learning methods. Comprehensive experiments reveal that the identified hierarchical emotional areas, from lower to higher levels, primarily facilitate the fundamental process of emotion perception, the construction of basic psychological operations, and the coordination and integration of these operations. Overall, our findings provide unique insights into the brain mechanisms underlying specific emotions based on the psychological constructionist hypothesis.

Going Deeper into Permutation-Sensitive Graph Neural Networks

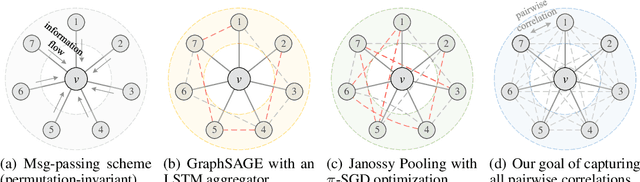
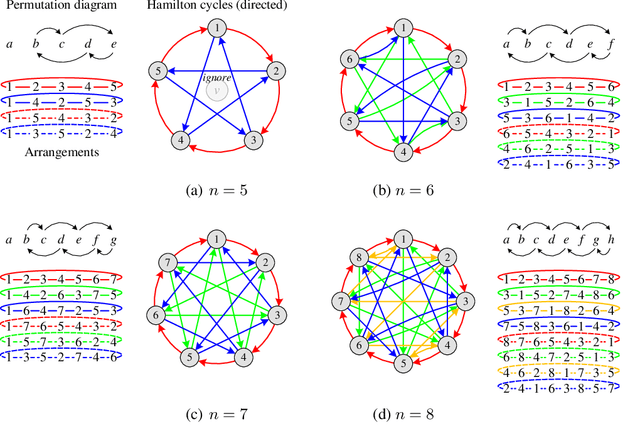
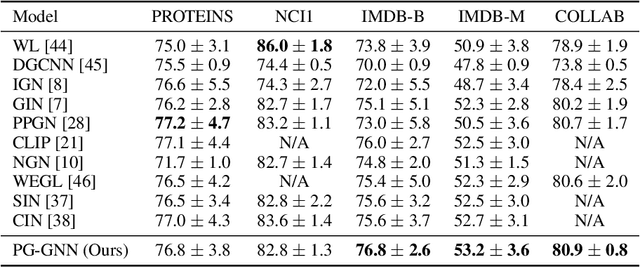
The invariance to permutations of the adjacency matrix, i.e., graph isomorphism, is an overarching requirement for Graph Neural Networks (GNNs). Conventionally, this prerequisite can be satisfied by the invariant operations over node permutations when aggregating messages. However, such an invariant manner may ignore the relationships among neighboring nodes, thereby hindering the expressivity of GNNs. In this work, we devise an efficient permutation-sensitive aggregation mechanism via permutation groups, capturing pairwise correlations between neighboring nodes. We prove that our approach is strictly more powerful than the 2-dimensional Weisfeiler-Lehman (2-WL) graph isomorphism test and not less powerful than the 3-WL test. Moreover, we prove that our approach achieves the linear sampling complexity. Comprehensive experiments on multiple synthetic and real-world datasets demonstrate the superiority of our model.