Going Deeper into Permutation-Sensitive Graph Neural Networks
Paper and Code
May 28, 2022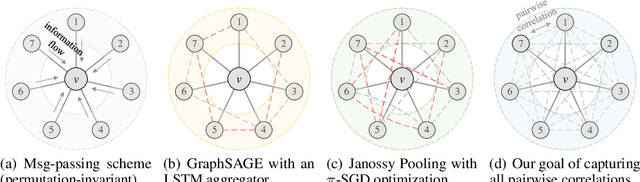
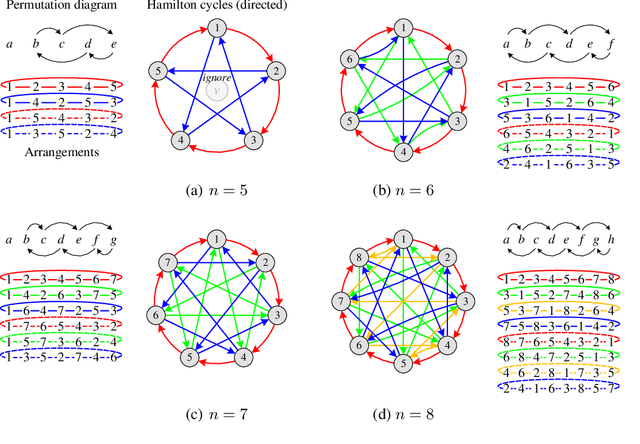

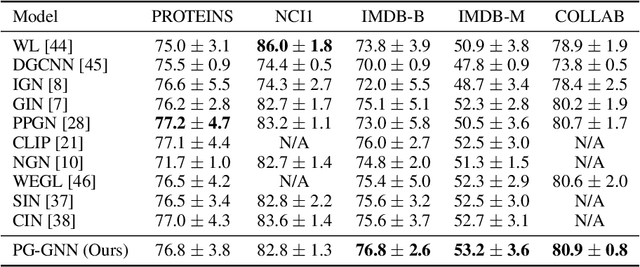
The invariance to permutations of the adjacency matrix, i.e., graph isomorphism, is an overarching requirement for Graph Neural Networks (GNNs). Conventionally, this prerequisite can be satisfied by the invariant operations over node permutations when aggregating messages. However, such an invariant manner may ignore the relationships among neighboring nodes, thereby hindering the expressivity of GNNs. In this work, we devise an efficient permutation-sensitive aggregation mechanism via permutation groups, capturing pairwise correlations between neighboring nodes. We prove that our approach is strictly more powerful than the 2-dimensional Weisfeiler-Lehman (2-WL) graph isomorphism test and not less powerful than the 3-WL test. Moreover, we prove that our approach achieves the linear sampling complexity. Comprehensive experiments on multiple synthetic and real-world datasets demonstrate the superiority of our model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge