Model Comparisons: XNet Outperforms KAN

In the fields of computational mathematics and artificial intelligence, the need for precise data modeling is crucial, especially for predictive machine learning tasks. This paper explores further XNet, a novel algorithm that employs the complex-valued Cauchy integral formula, offering a superior network architecture that surpasses traditional Multi-Layer Perceptrons (MLPs) and Kolmogorov-Arnold Networks (KANs). XNet significant improves speed and accuracy across various tasks in both low and high-dimensional spaces, redefining the scope of data-driven model development and providing substantial improvements over established time series models like LSTMs.

Leap-frog neural network for learning the symplectic evolution from partitioned data

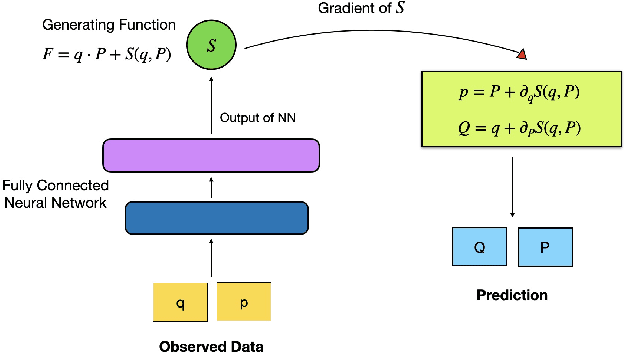
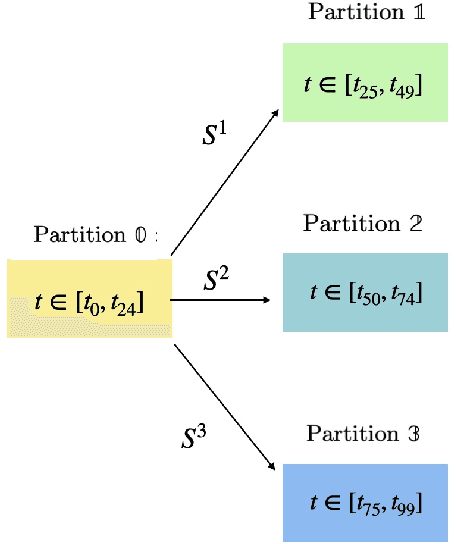
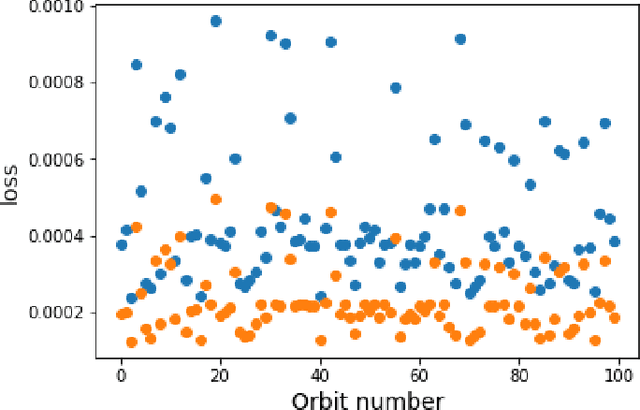
For the Hamiltonian system, this work considers the learning and prediction of the position (q) and momentum (p) variables generated by a symplectic evolution map. Similar to Chen & Tao (2021), the symplectic map is represented by the generating function. In addition, we develop a new learning scheme by splitting the time series (q_i, p_i) into several partitions, and then train a leap-frog neural network (LFNN) to approximate the generating function between the first (i.e. initial condition) and one of the rest partitions. For predicting the system evolution in a short timescale, the LFNN could effectively avoid the issue of accumulative error. Then the LFNN is applied to learn the behavior of the 2:3 resonant Kuiper belt objects, in a much longer time period, and there are two significant improvements on the neural network constructed in our previous work (Li et al. 2022): (1) conservation of the Jacobi integral ; (2) highly accurate prediction of the orbital evolution. We propose that the LFNN may be useful to make the prediction of the long time evolution of the Hamiltonian system.

Machine learning prediction for mean motion resonance behaviour -- The planar case

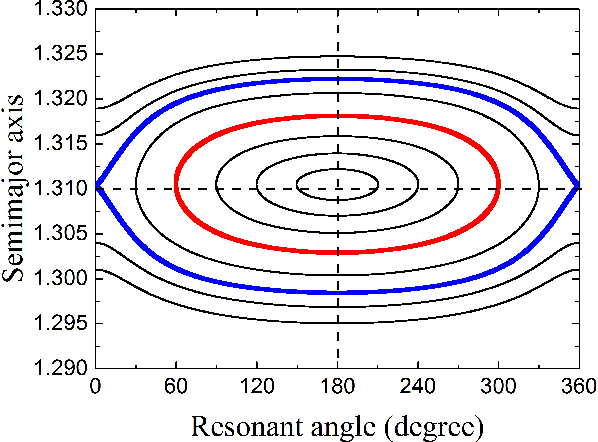
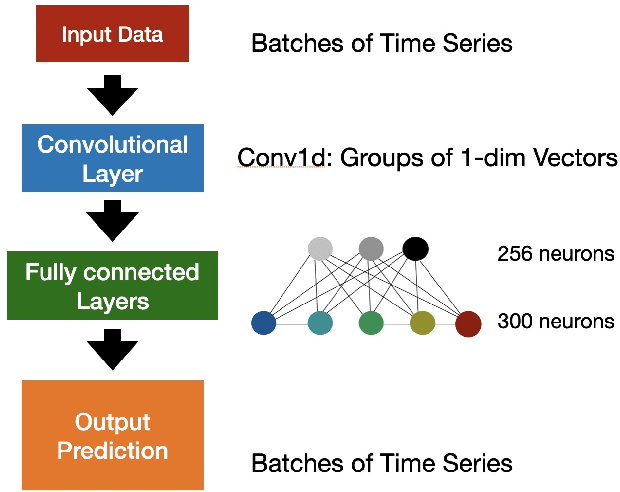
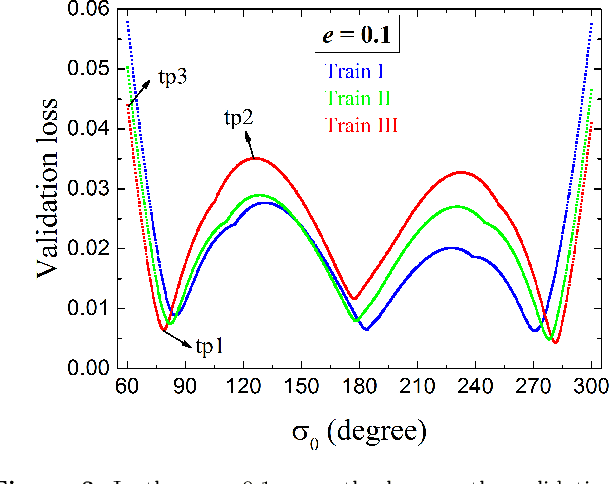
Most recently, machine learning has been used to study the dynamics of integrable Hamiltonian systems and the chaotic 3-body problem. In this work, we consider an intermediate case of regular motion in a non-integrable system: the behaviour of objects in the 2:3 mean motion resonance with Neptune. We show that, given initial data from a short 6250 yr numerical integration, the best-trained artificial neural network (ANN) can predict the trajectories of the 2:3 resonators over the subsequent 18750 yr evolution, covering a full libration cycle over the combined time period. By comparing our ANN's prediction of the resonant angle to the outcome of numerical integrations, the former can predict the resonant angle with an accuracy as small as of a few degrees only, while it has the advantage of considerably saving computational time. More specifically, the trained ANN can effectively measure the resonant amplitudes of the 2:3 resonators, and thus provides a fast approach that can identify the resonant candidates. This may be helpful in classifying a huge population of KBOs to be discovered in future surveys.