Leap-frog neural network for learning the symplectic evolution from partitioned data

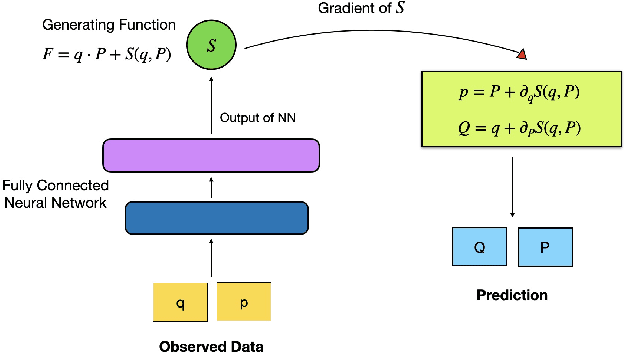
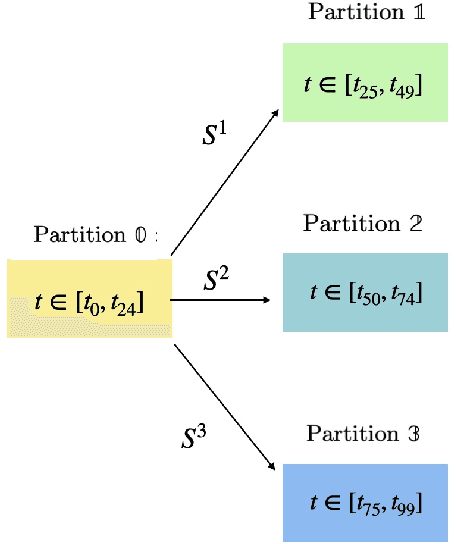
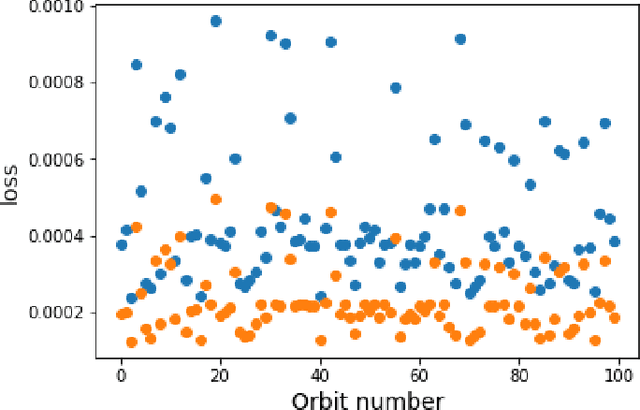
For the Hamiltonian system, this work considers the learning and prediction of the position (q) and momentum (p) variables generated by a symplectic evolution map. Similar to Chen & Tao (2021), the symplectic map is represented by the generating function. In addition, we develop a new learning scheme by splitting the time series (q_i, p_i) into several partitions, and then train a leap-frog neural network (LFNN) to approximate the generating function between the first (i.e. initial condition) and one of the rest partitions. For predicting the system evolution in a short timescale, the LFNN could effectively avoid the issue of accumulative error. Then the LFNN is applied to learn the behavior of the 2:3 resonant Kuiper belt objects, in a much longer time period, and there are two significant improvements on the neural network constructed in our previous work (Li et al. 2022): (1) conservation of the Jacobi integral ; (2) highly accurate prediction of the orbital evolution. We propose that the LFNN may be useful to make the prediction of the long time evolution of the Hamiltonian system.