Zhi-Zhong Liu
ATM-R: An Adaptive Tradeoff Model with Reference Points for Constrained Multiobjective Evolutionary Optimization
Jan 09, 2023



Abstract:The goal of constrained multiobjective evolutionary optimization is to obtain a set of well-converged and welldistributed feasible solutions. To complete this goal, there should be a tradeoff among feasibility, diversity, and convergence. However, it is nontrivial to balance these three elements simultaneously by using a single tradeoff model since the importance of each element varies in different evolutionary phases. As an alternative, we adapt different tradeoff models in different phases and propose a novel algorithm called ATM-R. In the infeasible phase, ATM-R takes the tradeoff between diversity and feasibility into account, aiming to move the population toward feasible regions from diverse search directions. In the semi-feasible phase, ATM-R promotes the transition from "the tradeoff between feasibility and diversity" to "the tradeoff between diversity and convergence", which can facilitate the discovering of enough feasible regions and speed up the search for the feasible Pareto optima in succession. In the feasible phase, the tradeoff between diversity and convergence is considered to attain a set of well-converged and well-distributed feasible solutions. It is worth noting that the merits of reference points are leveraged in ATM-R to accomplish these tradeoff models. Also, in ATM-R, a multiphase mating selection strategy is developed to generate promising solutions beneficial to different evolutionary phases. Systemic experiments on a wide range of benchmark test functions demonstrate that ATM-R is effective and competitive, compared against five state-of-the-art constrained multiobjective optimization evolutionary algorithms.
A Many-Objective Evolutionary Algorithm with Angle-Based Selection and Shift-Based Density Estimation
Sep 30, 2017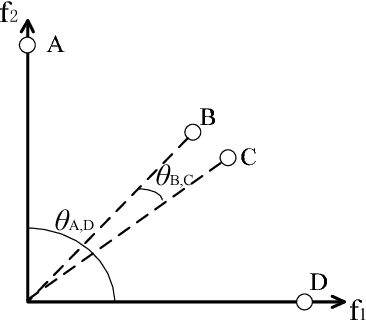
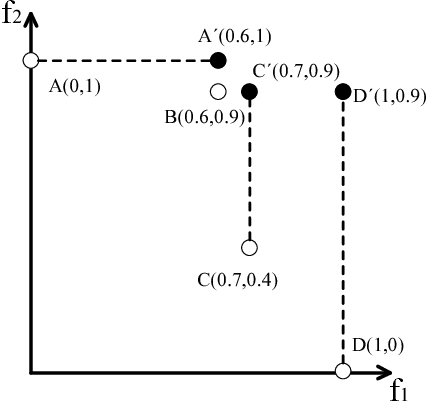
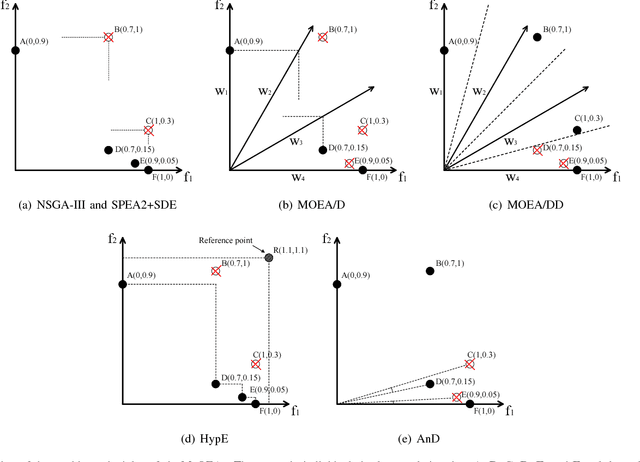
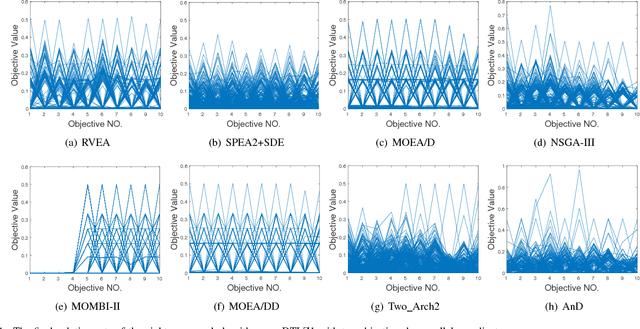
Abstract:Evolutionary many-objective optimization has been gaining increasing attention from the evolutionary computation research community. Much effort has been devoted to addressing this issue by improving the scalability of multiobjective evolutionary algorithms, such as Pareto-based, decomposition-based, and indicator-based approaches. Different from current work, we propose a novel algorithm in this paper called AnD, which consists of an angle-based selection strategy and a shift-based density estimation strategy. These two strategies are employed in the environmental selection to delete the poor individuals one by one. Specifically, the former is devised to find a pair of individuals with the minimum vector angle, which means that these two individuals share the most similar search direction. The latter, which takes both the diversity and convergence into account, is adopted to compare these two individuals and to delete the worse one. AnD has a simple structure, few parameters, and no complicated operators. The performance of AnD is compared with that of seven state-of-the-art many-objective evolutionary algorithms on a variety of benchmark test problems with up to 15 objectives. The experimental results suggest that AnD can achieve highly competitive performance. In addition, we also verify that AnD can be readily extended to solve constrained many-objective optimization problems.
An Adaptive Framework to Tune the Coordinate Systems in Evolutionary Algorithms
Mar 18, 2017



Abstract:In the evolutionary computation research community, the performance of most evolutionary algorithms (EAs) depends strongly on their implemented coordinate system. However, the commonly used coordinate system is fixed and not well suited for different function landscapes, EAs thus might not search efficiently. To overcome this shortcoming, in this paper we propose a framework, named ACoS, to adaptively tune the coordinate systems in EAs. In ACoS, an Eigen coordinate system is established by making use of the cumulative population distribution information, which can be obtained based on a covariance matrix adaptation strategy and an additional archiving mechanism. Since the population distribution information can reflect the features of the function landscape to some extent, EAs in the Eigen coordinate system have the capability to identify the modality of the function landscape. In addition, the Eigen coordinate system is coupled with the original coordinate system, and they are selected according to a probability vector. The probability vector aims to determine the selection ratio of each coordinate system for each individual, and is adaptively updated based on the collected information from the offspring. ACoS has been applied to two of the most popular EA paradigms, i.e., particle swarm optimization (PSO) and differential evolution (DE), for solving 30 test functions with 30 and 50 dimensions at the 2014 IEEE Congress on Evolutionary Computation. The experimental studies demonstrate its effectiveness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge