Significant Wave Height Prediction based on Wavelet Graph Neural Network

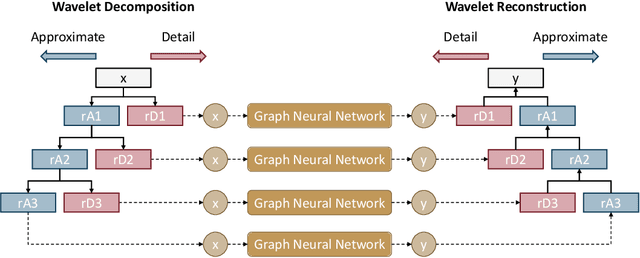
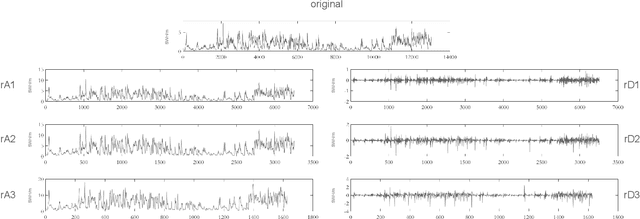
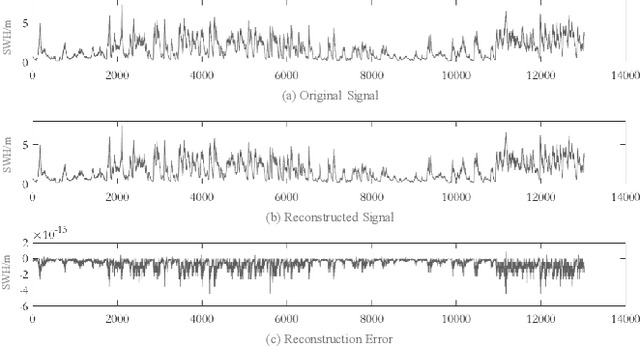
Computational intelligence-based ocean characteristics forecasting applications, such as Significant Wave Height (SWH) prediction, are crucial for avoiding social and economic loss in coastal cities. Compared to the traditional empirical-based or numerical-based forecasting models, "soft computing" approaches, including machine learning and deep learning models, have shown numerous success in recent years. In this paper, we focus on enabling the deep learning model to learn both short-term and long-term spatial-temporal dependencies for SWH prediction. A Wavelet Graph Neural Network (WGNN) approach is proposed to integrate the advantages of wavelet transform and graph neural network. Several parallel graph neural networks are separately trained on wavelet decomposed data, and the reconstruction of each model's prediction forms the final SWH prediction. Experimental results show that the proposed WGNN approach outperforms other models, including the numerical models, the machine learning models, and several deep learning models.

Extended Gauss-Newton and Gauss-Newton-ADMM Algorithms for Low-Rank Matrix Optimization

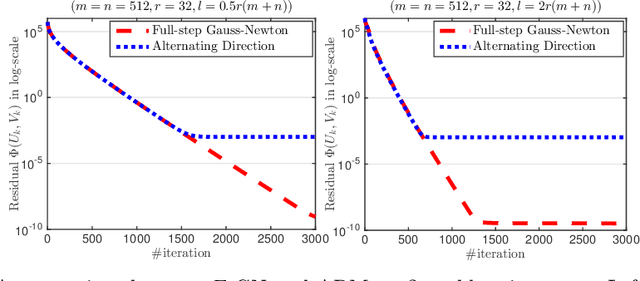
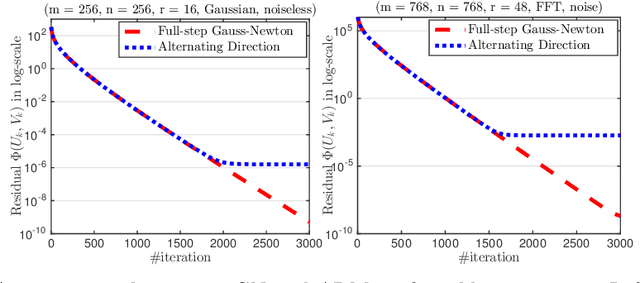
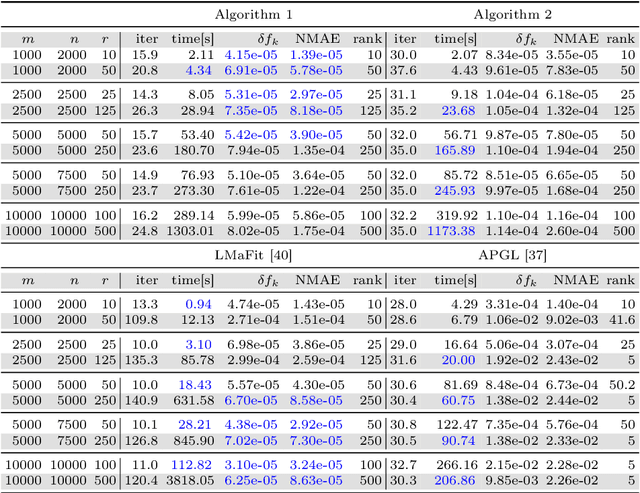
We develop a generic Gauss-Newton (GN) framework for solving a class of nonconvex optimization problems involving low-rank matrix variables. As opposed to standard Gauss-Newton method, our framework allows one to handle general smooth convex cost function via its surrogate. The main complexity-per-iteration consists of the inverse of two rank-size matrices and at most six small matrix multiplications to compute a closed form Gauss-Newton direction, and a backtracking linesearch. We show, under mild conditions, that the proposed algorithm globally and locally converges to a stationary point of the original nonconvex problem. We also show empirically that the Gauss-Newton algorithm achieves much higher accurate solutions compared to the well studied alternating direction method (ADM). Then, we specify our Gauss-Newton framework to handle the symmetric case and prove its convergence, where ADM is not applicable without lifting variables. Next, we incorporate our Gauss-Newton scheme into the alternating direction method of multipliers (ADMM) to design a GN-ADMM algorithm for solving the low-rank optimization problem. We prove that, under mild conditions and a proper choice of the penalty parameter, our GN-ADMM globally converges to a stationary point of the original problem. Finally, we apply our algorithms to solve several problems in practice such as low-rank approximation, matrix completion, robust low-rank matrix recovery, and matrix recovery in quantum tomography. The numerical experiments provide encouraging results to motivate the use of nonconvex optimization.