A Homotopy Coordinate Descent Optimization Method for $l_0$-Norm Regularized Least Square Problem

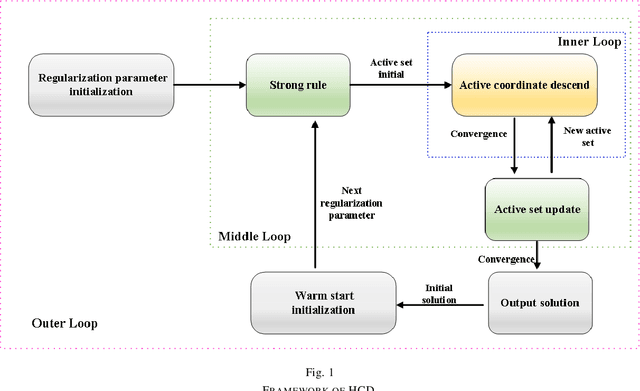
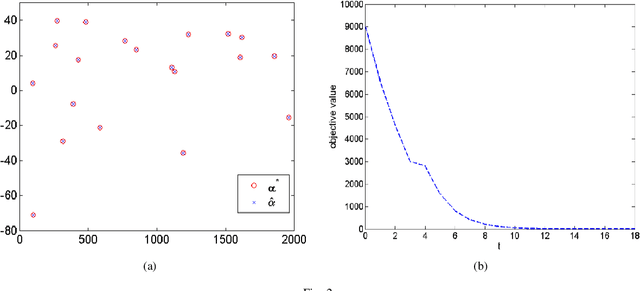
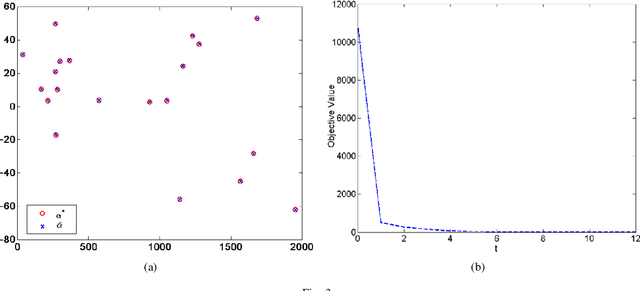
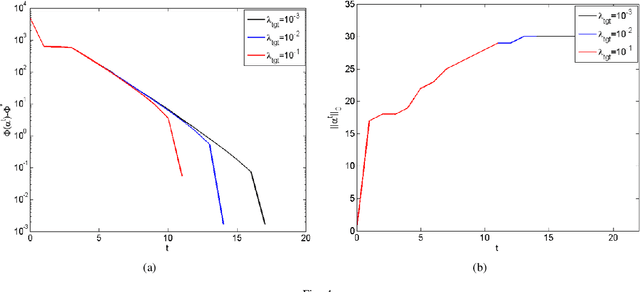
This paper proposes a homotopy coordinate descent (HCD) method to solve the $l_0$-norm regularized least square ($l_0$-LS) problem for compressed sensing, which combine the homotopy technique with a variant of coordinate descent method. Differs from the classical coordinate descent algorithms, HCD provides three strategies to speed up the convergence: warm start initialization, active set updating, and strong rule for active set initialization. The active set is pre-selected using a strong rule, then the coordinates of the active set are updated while those of inactive set are unchanged. The homotopy strategy provides a set of warm start initial solutions for a sequence of decreasing values of the regularization factor, which ensures all iterations along the homotopy solution path are sparse. Computational experiments on simulate signals and natural signals demonstrate effectiveness of the proposed algorithm, in accurately and efficiently reconstructing sparse solutions of the $l_0$-LS problem, whether the observation is noisy or not.

Nonnegative Spectral Analysis with Adaptive Graph and $L_{2,0}$-Norm Regularization for Unsupervised Feature Selection

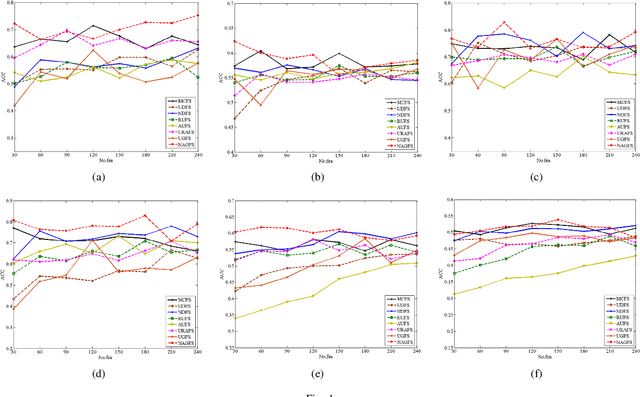
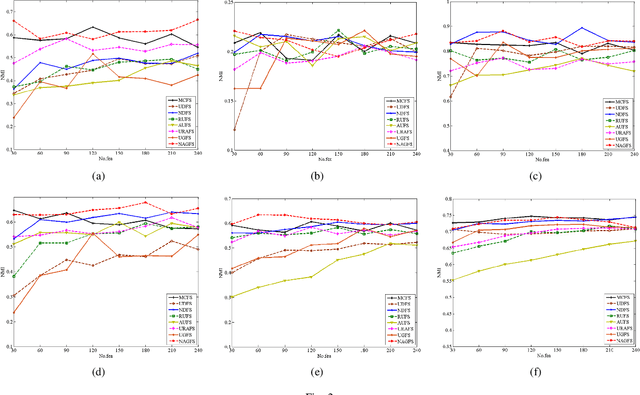
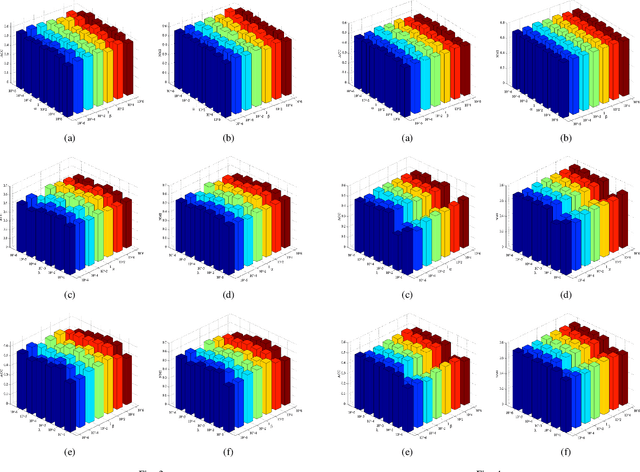
Feature selection is used to reduce feature dimension while maintain model's performance, which has been an important data preprocessing in many fields. Since obtaining annotated data is laborious or even infeasible in many cases, unsupervised feature selection is more practical in reality. Although a lots of methods have been proposed, these methods select features independently, thus it is no guarantee that the group of selected features is optimal. What's more, the number of selected features must be tuned carefully to get a satisfactory result. In this paper, we propose a novel unsupervised feature selection method which incorporate spectral analysis with a $l_{2,0}$-norm regularized term. After optimization, a group of optimal features will be selected, and the number of selected features will be determined automatically. What's more, a nonnegative constraint with respect to the class indicators is imposed to learn more accurate cluster labels, and a graph regularized term is added to learn the similarity matrix adaptively. An efficient and simple iterative algorithm is designed to optimize the proposed problem. Experiments on six different benchmark data sets validate the effectiveness of the proposed approach.

Robust Multi-class Feature Selection via $l_{2,0}$-Norm Regularization Minimization

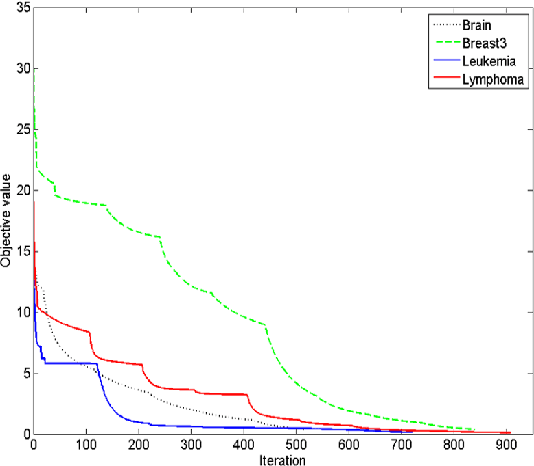
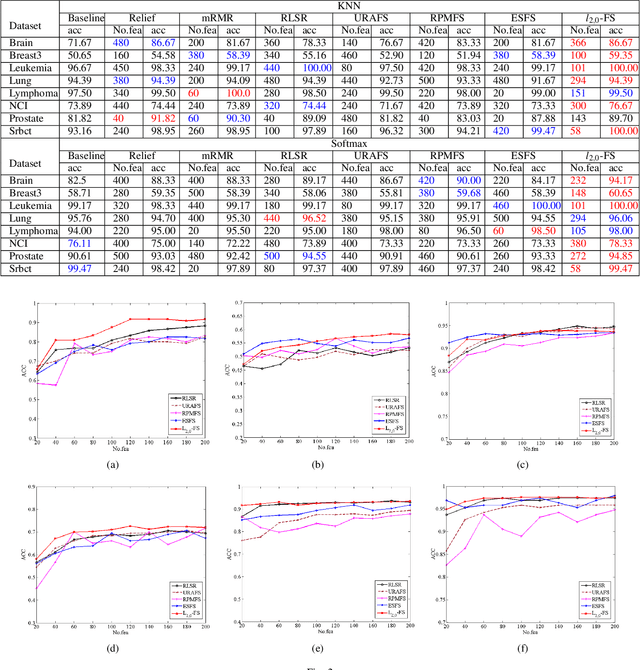
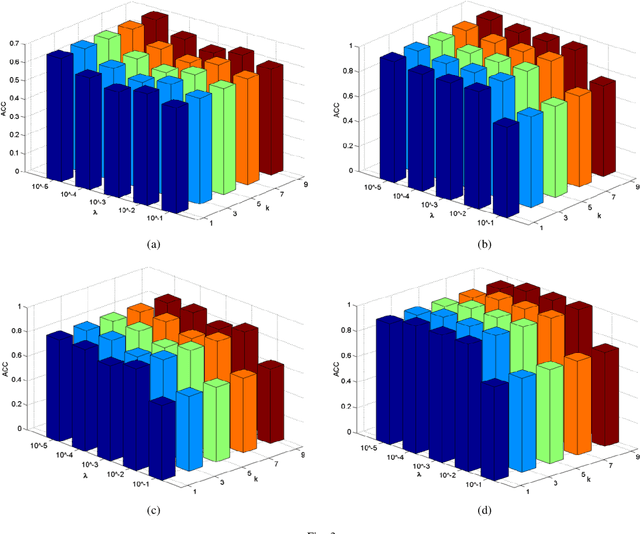
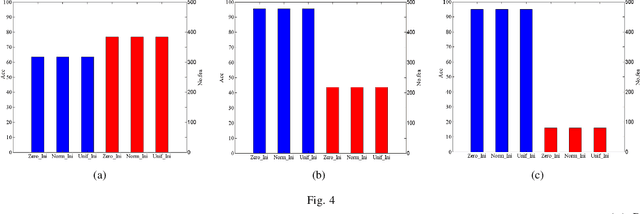
Feature selection is an important data preprocessing in data mining and machine learning, which can reduce feature size without deteriorating model's performance. Recently, sparse regression based feature selection methods have received considerable attention due to their good performance. However, these methods generally cannot determine the number of selected features automatically without using a predefined threshold. In order to get a satisfactory result, it often costs significant time and effort to tune the number of selected features carefully. To this end, this paper proposed a novel framework to solve the $l_{2,0}$-norm regularization least square problem directly for multi-class feature selection, which can produce exact rowsparsity solution for the weights matrix, features corresponding to non-zero rows will be selected thus the number of selected features can be determined automatically. An efficient homotopy iterative hard threshold (HIHT) algorithm is derived to solve the above optimization problem and find out the stable local solution. Besides, in order to reduce the computational time of HIHT, an acceleration version of HIHT (AHIHT) is derived. Extensive experiments on eight biological datasets show that the proposed method can achieve higher classification accuracy with fewest number of selected features comparing with the approximate convex counterparts and state-of-the-art feature selection methods. The robustness of classification accuracy to the regularization parameter is also exhibited.