Robust Multi-class Feature Selection via $l_{2,0}$-Norm Regularization Minimization

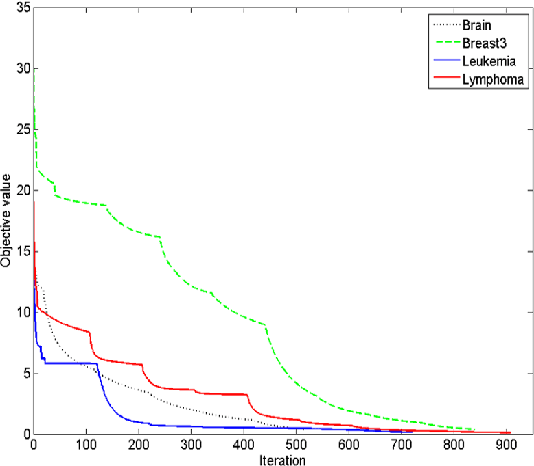
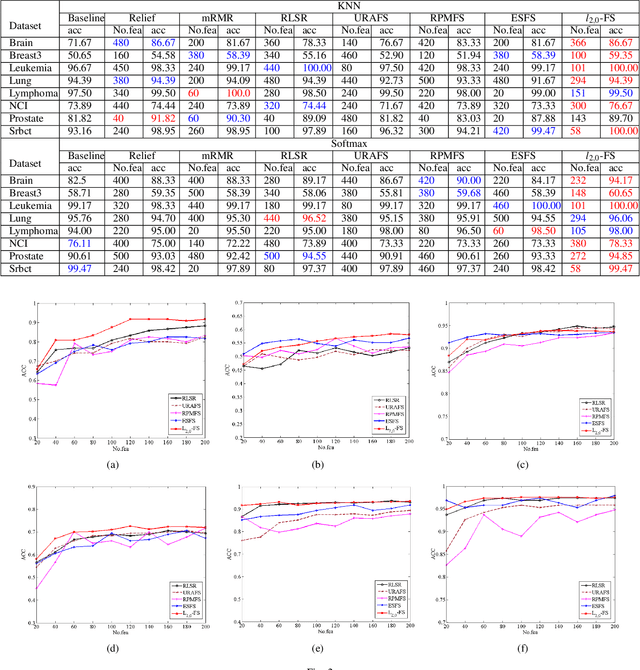
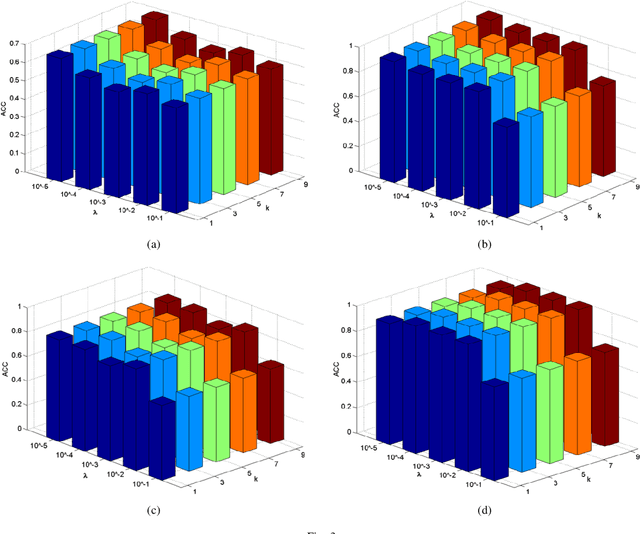
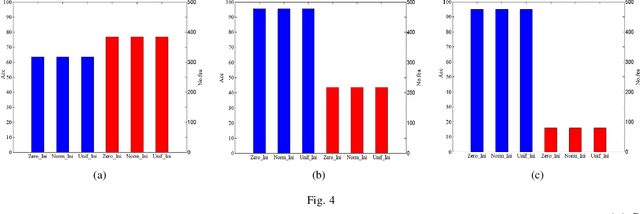
Feature selection is an important data preprocessing in data mining and machine learning, which can reduce feature size without deteriorating model's performance. Recently, sparse regression based feature selection methods have received considerable attention due to their good performance. However, these methods generally cannot determine the number of selected features automatically without using a predefined threshold. In order to get a satisfactory result, it often costs significant time and effort to tune the number of selected features carefully. To this end, this paper proposed a novel framework to solve the $l_{2,0}$-norm regularization least square problem directly for multi-class feature selection, which can produce exact rowsparsity solution for the weights matrix, features corresponding to non-zero rows will be selected thus the number of selected features can be determined automatically. An efficient homotopy iterative hard threshold (HIHT) algorithm is derived to solve the above optimization problem and find out the stable local solution. Besides, in order to reduce the computational time of HIHT, an acceleration version of HIHT (AHIHT) is derived. Extensive experiments on eight biological datasets show that the proposed method can achieve higher classification accuracy with fewest number of selected features comparing with the approximate convex counterparts and state-of-the-art feature selection methods. The robustness of classification accuracy to the regularization parameter is also exhibited.