Variable Selection and Regularization via Arbitrary Rectangle-range Generalized Elastic Net

We introduce the arbitrary rectangle-range generalized elastic net penalty method, abbreviated to ARGEN, for performing constrained variable selection and regularization in high-dimensional sparse linear models. As a natural extension of the nonnegative elastic net penalty method, ARGEN is proved to have variable selection consistency and estimation consistency under some conditions. The asymptotic behavior in distribution of the ARGEN estimators have been studied. We also propose an algorithm called MU-QP-RR-W-$l_1$ to efficiently solve ARGEN. By conducting simulation study we show that ARGEN outperforms the elastic net in a number of settings. Finally an application of S&P 500 index tracking with constraints on the stock allocations is performed to provide general guidance for adapting ARGEN to solve real-world problems.

Learning to fail: Predicting fracture evolution in brittle materials using recurrent graph convolutional neural networks

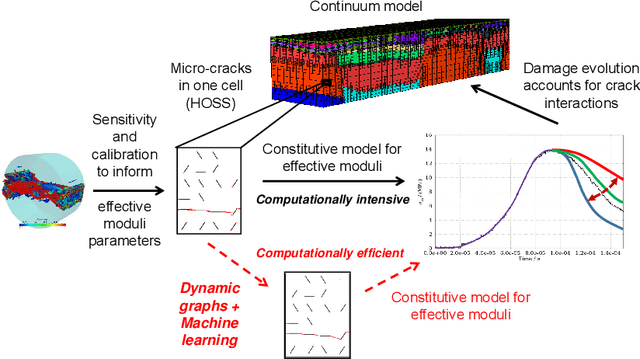
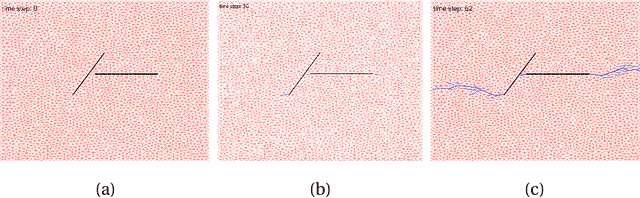
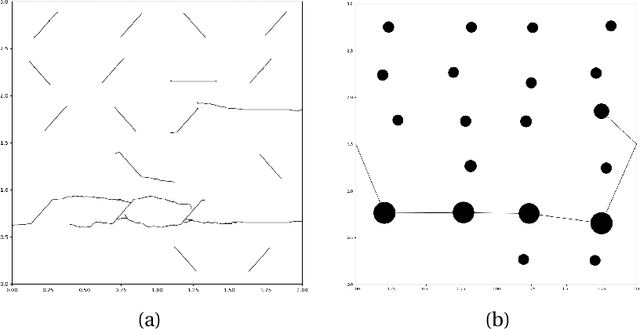
Understanding dynamic fracture propagation is essential to predicting how brittle materials fail. Various mathematical models and computational applications have been developed to predict fracture evolution and coalescence, including finite-discrete element methods such as the Hybrid Optimization Software Suite (HOSS). While such methods achieve high fidelity results, they can be computationally prohibitive: a single simulation takes hours to run, and thousands of simulations are required for a statistically meaningful ensemble. We propose a machine learning approach that, once trained on data from HOSS simulations, can predict fracture growth statistics within seconds. Our method uses deep learning, exploiting the capabilities of a graph convolutional network to recognize features of the fracturing material, along with a recurrent neural network to model the evolution of these features. In this way, we simultaneously generate predictions for qualitatively distinct material properties. Our prediction for total damage in a coalesced fracture, at the final simulation time step, is within 3% of its actual value, and our prediction for total length of a coalesced fracture is within 2%. We also develop a novel form of data augmentation that compensates for the modest size of our training data, and an ensemble learning approach that enables us to predict when the material fails, with a mean absolute error of approximately 15%.