Zhejun Huang
Manifold Regularized Tucker Decomposition Approach for Spatiotemporal Traffic Data Imputation
May 16, 2023Abstract:Spatiotemporal traffic data imputation (STDI), estimating the missing data from partially observed traffic data, is an inevitable and challenging task in data-driven intelligent transportation systems (ITS). Due to traffic data's multidimensional and spatiotemporal properties, we treat the missing data imputation as a tensor completion problem. Many studies have been on STDI based on tensor decomposition in the past decade. However, how to use spatiotemporal correlations and core tensor sparsity to improve the imputation performance still needs to be solved. This paper reshapes a 3rd/4th order Hankel tensor and proposes an innovative manifold regularized Tucker decomposition (ManiRTD) model for STDI. Expressly, we represent the sensory traffic state data as the 3rd/4th tensors by introducing Multiway Delay Embedding Transforms. Then, ManiRTD improves the sparsity of the Tucker core using a sparse regularization term and employs manifold regularization and temporal constraint terms of factor matrices to characterize the spatiotemporal correlations. Finally, we address the ManiRTD model through a block coordinate descent framework under alternating proximal gradient updating rules with convergence-guaranteed. Numerical experiments are conducted on real-world spatiotemporal traffic datasets (STDs). Our results demonstrate that the proposed model outperforms the other factorization approaches and reconstructs the STD more precisely under various missing scenarios.
Sparse Gaussian Process Based On Hat Basis Functions
Jun 15, 2020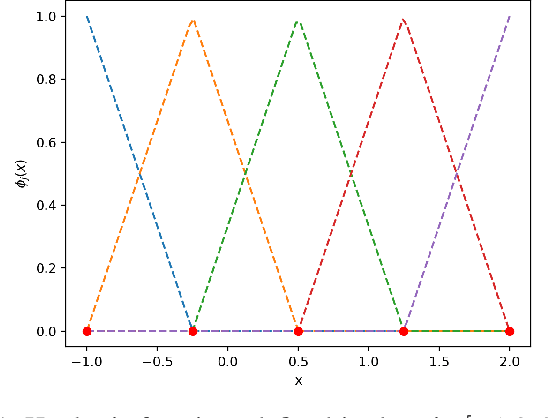
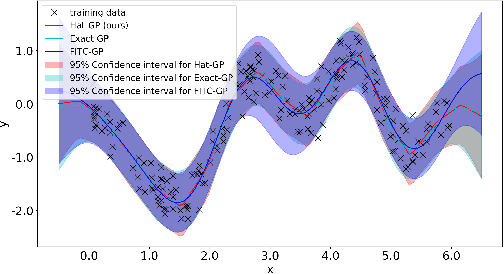
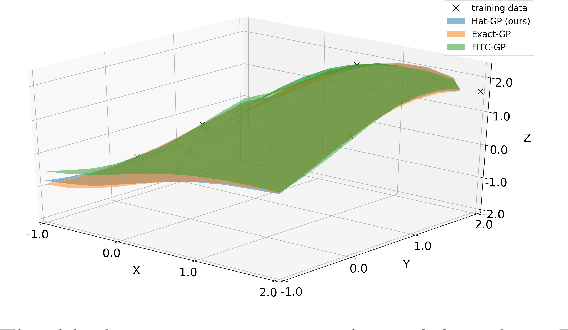
Abstract:Gaussian process is one of the most popular non-parametric Bayesian methodologies for modeling the regression problem. It is completely determined by its mean and covariance functions. And its linear property makes it relatively straightforward to solve the prediction problem. Although Gaussian process has been successfully applied in many fields, it is still not enough to deal with physical systems that satisfy inequality constraints. This issue has been addressed by the so-called constrained Gaussian process in recent years. In this paper, we extend the core ideas of constrained Gaussian process. According to the range of training or test data, we redefine the hat basis functions mentioned in the constrained Gaussian process. Based on hat basis functions, we propose a new sparse Gaussian process method to solve the unconstrained regression problem. Similar to the exact Gaussian process and Gaussian process with Fully Independent Training Conditional approximation, our method obtains satisfactory approximate results on open-source datasets or analytical functions. In terms of performance, the proposed method reduces the overall computational complexity from $O(n^{3})$ computation in exact Gaussian process to $O(nm^{2})$ with $m$ hat basis functions and $n$ training data points.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge