ModRWKV: Transformer Multimodality in Linear Time

Currently, most multimodal studies are based on large language models (LLMs) with quadratic-complexity Transformer architectures. While linear models like RNNs enjoy low inference costs, their application has been largely limited to the text-only modality. This work explores the capabilities of modern RNN architectures in multimodal contexts. We propose ModRWKV-a decoupled multimodal framework built upon the RWKV7 architecture as its LLM backbone-which achieves multi-source information fusion through dynamically adaptable heterogeneous modality encoders. We designed the multimodal modules in ModRWKV with an extremely lightweight architecture and, through extensive experiments, identified a configuration that achieves an optimal balance between performance and computational efficiency. ModRWKV leverages the pretrained weights of the RWKV7 LLM for initialization, which significantly accelerates multimodal training. Comparative experiments with different pretrained checkpoints further demonstrate that such initialization plays a crucial role in enhancing the model's ability to understand multimodal signals. Supported by extensive experiments, we conclude that modern RNN architectures present a viable alternative to Transformers in the domain of multimodal large language models (MLLMs). Furthermore, we identify the optimal configuration of the ModRWKV architecture through systematic exploration.

Low Dose CT Image Reconstruction With Learned Sparsifying Transform

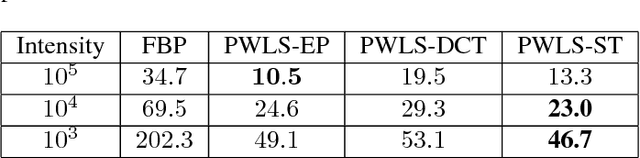
A major challenge in computed tomography (CT) is to reduce X-ray dose to a low or even ultra-low level while maintaining the high quality of reconstructed images. We propose a new method for CT reconstruction that combines penalized weighted-least squares reconstruction (PWLS) with regularization based on a sparsifying transform (PWLS-ST) learned from a dataset of numerous CT images. We adopt an alternating algorithm to optimize the PWLS-ST cost function that alternates between a CT image update step and a sparse coding step. We adopt a relaxed linearized augmented Lagrangian method with ordered-subsets (relaxed OS-LALM) to accelerate the CT image update step by reducing the number of forward and backward projections. Numerical experiments on the XCAT phantom show that for low dose levels, the proposed PWLS-ST method dramatically improves the quality of reconstructed images compared to PWLS reconstruction with a nonadaptive edge-preserving regularizer (PWLS-EP).