Zengyue Guo
NNCFR: Minimize Counterfactual Regret with Neural Networks
May 26, 2021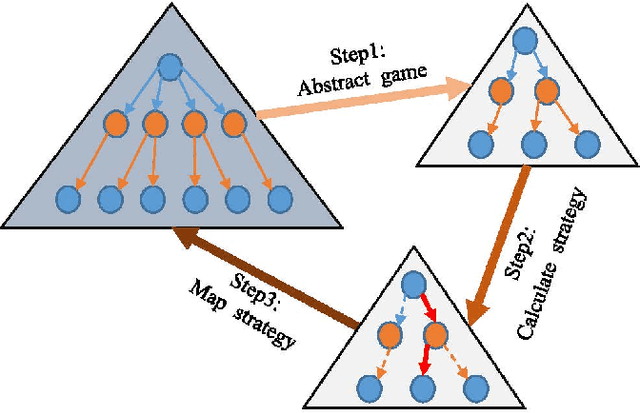

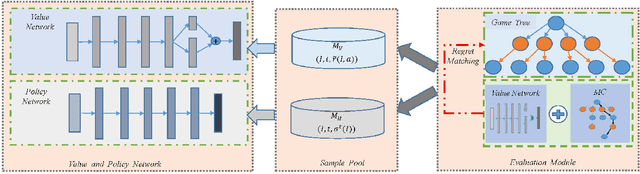
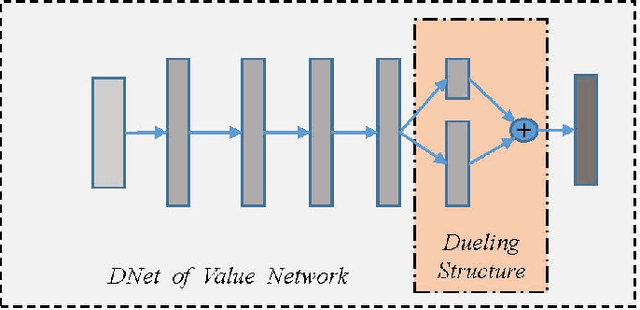
Abstract:Counterfactual Regret Minimization (CFR)} is the popular method for finding approximate Nash equilibrium in two-player zero-sum games with imperfect information. CFR solves games by travsersing the full game tree iteratively, which limits its scalability in larger games. When applying CFR to solve large-scale games in previously, large-scale games are abstracted into small-scale games firstly. Secondly, CFR is used to solve the abstract game. And finally, the solution strategy is mapped back to the original large-scale game. However, this process requires considerable expert knowledge, and the accuracy of abstraction is closely related to expert knowledge. In addition, the abstraction also loses certain information, which will eventually affect the accuracy of the solution strategy. Towards this problem, a recent method, \textit{Deep CFR} alleviates the need for abstraction and expert knowledge by applying deep neural networks directly to CFR in full games. In this paper, we introduces \textit{Neural Network Counterfactual Regret Minimization (NNCFR)}, an improved variant of \textit{Deep CFR} that has a faster convergence by constructing a dueling netwok as the value network. Moreover, an evaluation module is designed by combining the value network and Monte Carlo, which reduces the approximation error of the value network. In addition, a new loss function is designed in the procedure of training policy network in the proposed \textit{NNCFR}, which can be good to make the policy network more stable. The extensive experimental tests are conducted to show that the \textit{NNCFR} converges faster and performs more stable than \textit{Deep CFR}, and outperforms \textit{Deep CFR} with respect to exploitability and head-to-head performance on test games.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge