Global Minima, Recoverability Thresholds, and Higher-Order Structure in GNNS

We analyze the performance of graph neural network (GNN) architectures from the perspective of random graph theory. Our approach promises to complement existing lenses on GNN analysis, such as combinatorial expressive power and worst-case adversarial analysis, by connecting the performance of GNNs to typical-case properties of the training data. First, we theoretically characterize the nodewise accuracy of one- and two-layer GCNs relative to the contextual stochastic block model (cSBM) and related models. We additionally prove that GCNs cannot beat linear models under certain circumstances. Second, we numerically map the recoverability thresholds, in terms of accuracy, of four diverse GNN architectures (GCN, GAT, SAGE, and Graph Transformer) under a variety of assumptions about the data. Sample results of this second analysis include: heavy-tailed degree distributions enhance GNN performance, GNNs can work well on strongly heterophilous graphs, and SAGE and Graph Transformer can perform well on arbitrarily noisy edge data, but no architecture handled sufficiently noisy feature data well. Finally, we show how both specific higher-order structures in synthetic data and the mix of empirical structures in real data have dramatic effects (usually negative) on GNN performance.

Simplified Energy Landscape for Modularity Using Total Variation

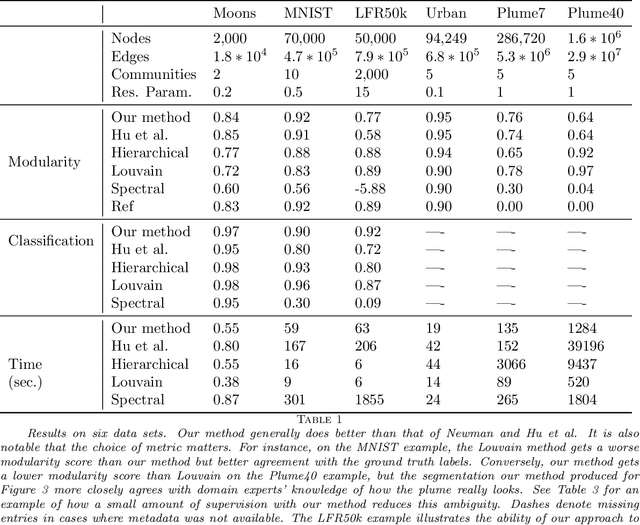
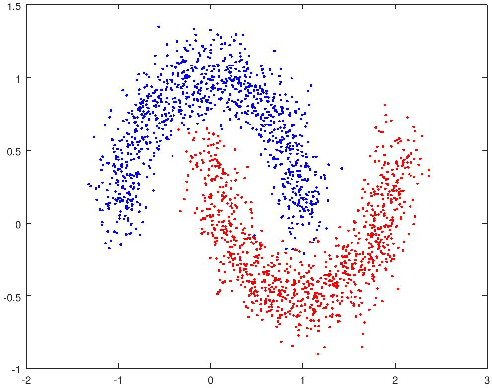
Networks capture pairwise interactions between entities and are frequently used in applications such as social networks, food networks, and protein interaction networks, to name a few. Communities, cohesive groups of nodes, often form in these applications, and identifying them gives insight into the overall organization of the network. One common quality function used to identify community structure is modularity. In Hu et al. [SIAM J. App. Math., 73(6), 2013], it was shown that modularity optimization is equivalent to minimizing a particular nonconvex total variation (TV) based functional over a discrete domain. They solve this problem, assuming the number of communities is known, using a Merriman, Bence, Osher (MBO) scheme. We show that modularity optimization is equivalent to minimizing a convex TV-based functional over a discrete domain, again, assuming the number of communities is known. Furthermore, we show that modularity has no convex relaxation satisfying certain natural conditions. We therefore, find a manageable non-convex approximation using a Ginzburg Landau functional, which provably converges to the correct energy in the limit of a certain parameter. We then derive an MBO algorithm with fewer hand-tuned parameters than in Hu et al. and which is 7 times faster at solving the associated diffusion equation due to the fact that the underlying discretization is unconditionally stable. Our numerical tests include a hyperspectral video whose associated graph has 2.9x10^7 edges, which is roughly 37 times larger than was handled in the paper of Hu et al.