The Mysterious Case of Neuron 1512: Injectable Realignment Architectures Reveal Internal Characteristics of Meta's Llama 2 Model

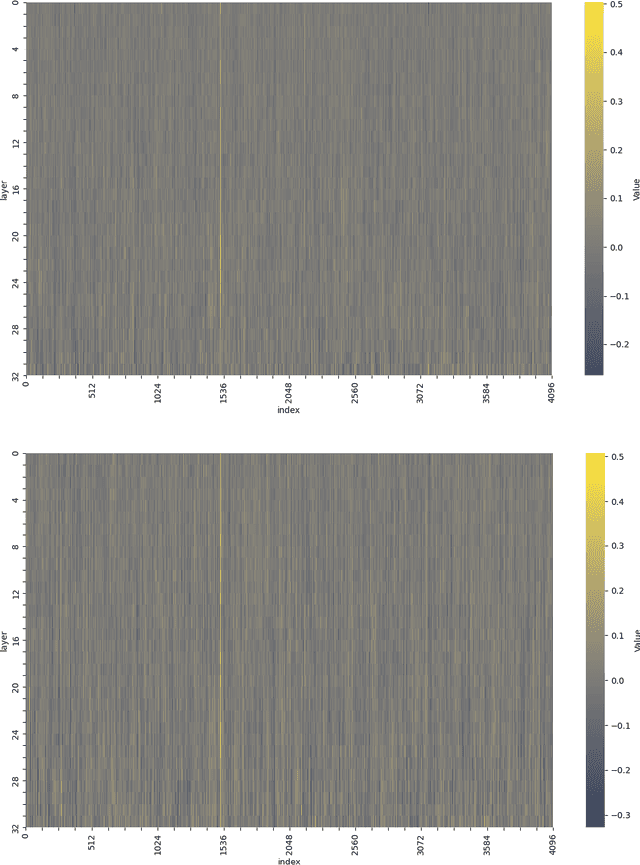
Large Language Models (LLMs) have an unrivaled and invaluable ability to "align" their output to a diverse range of human preferences, by mirroring them in the text they generate. The internal characteristics of such models, however, remain largely opaque. This work presents the Injectable Realignment Model (IRM) as a novel approach to language model interpretability and explainability. Inspired by earlier work on Neural Programming Interfaces, we construct and train a small network -- the IRM -- to induce emotion-based alignments within a 7B parameter LLM architecture. The IRM outputs are injected via layerwise addition at various points during the LLM's forward pass, thus modulating its behavior without changing the weights of the original model. This isolates the alignment behavior from the complex mechanisms of the transformer model. Analysis of the trained IRM's outputs reveals a curious pattern. Across more than 24 training runs and multiple alignment datasets, patterns of IRM activations align themselves in striations associated with a neuron's index within each transformer layer, rather than being associated with the layers themselves. Further, a single neuron index (1512) is strongly correlated with all tested alignments. This result, although initially counterintuitive, is directly attributable to design choices present within almost all commercially available transformer architectures, and highlights a potential weak point in Meta's pretrained Llama 2 models. It also demonstrates the value of the IRM architecture for language model analysis and interpretability. Our code and datasets are available at https://github.com/DRAGNLabs/injectable-alignment-model

Global Minima, Recoverability Thresholds, and Higher-Order Structure in GNNS

We analyze the performance of graph neural network (GNN) architectures from the perspective of random graph theory. Our approach promises to complement existing lenses on GNN analysis, such as combinatorial expressive power and worst-case adversarial analysis, by connecting the performance of GNNs to typical-case properties of the training data. First, we theoretically characterize the nodewise accuracy of one- and two-layer GCNs relative to the contextual stochastic block model (cSBM) and related models. We additionally prove that GCNs cannot beat linear models under certain circumstances. Second, we numerically map the recoverability thresholds, in terms of accuracy, of four diverse GNN architectures (GCN, GAT, SAGE, and Graph Transformer) under a variety of assumptions about the data. Sample results of this second analysis include: heavy-tailed degree distributions enhance GNN performance, GNNs can work well on strongly heterophilous graphs, and SAGE and Graph Transformer can perform well on arbitrarily noisy edge data, but no architecture handled sufficiently noisy feature data well. Finally, we show how both specific higher-order structures in synthetic data and the mix of empirical structures in real data have dramatic effects (usually negative) on GNN performance.