Yuta Hozumi
Enhancing Satellite Object Localization with Dilated Convolutions and Attention-aided Spatial Pooling
May 08, 2025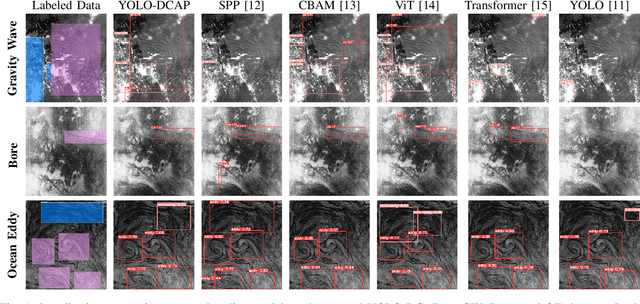
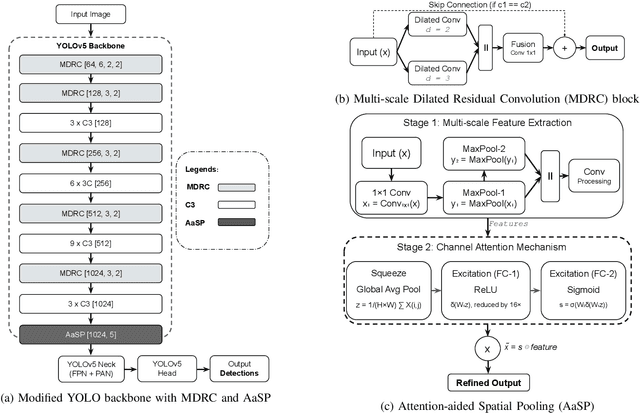
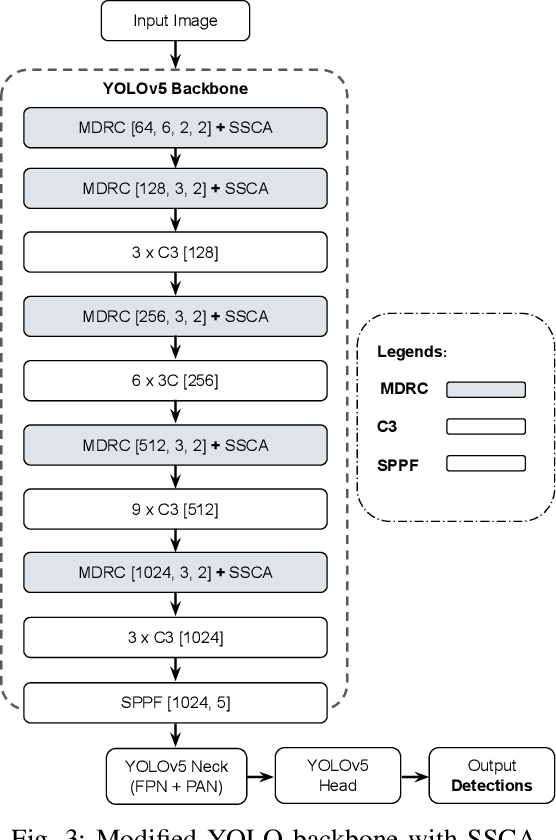
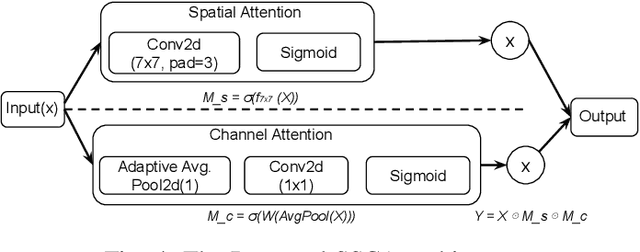
Abstract:Object localization in satellite imagery is particularly challenging due to the high variability of objects, low spatial resolution, and interference from noise and dominant features such as clouds and city lights. In this research, we focus on three satellite datasets: upper atmospheric Gravity Waves (GW), mesospheric Bores (Bore), and Ocean Eddies (OE), each presenting its own unique challenges. These challenges include the variability in the scale and appearance of the main object patterns, where the size, shape, and feature extent of objects of interest can differ significantly. To address these challenges, we introduce YOLO-DCAP, a novel enhanced version of YOLOv5 designed to improve object localization in these complex scenarios. YOLO-DCAP incorporates a Multi-scale Dilated Residual Convolution (MDRC) block to capture multi-scale features at scale with varying dilation rates, and an Attention-aided Spatial Pooling (AaSP) module to focus on the global relevant spatial regions, enhancing feature selection. These structural improvements help to better localize objects in satellite imagery. Experimental results demonstrate that YOLO-DCAP significantly outperforms both the YOLO base model and state-of-the-art approaches, achieving an average improvement of 20.95% in mAP50 and 32.23% in IoU over the base model, and 7.35% and 9.84% respectively over state-of-the-art alternatives, consistently across all three satellite datasets. These consistent gains across all three satellite datasets highlight the robustness and generalizability of the proposed approach. Our code is open sourced at https://github.com/AI-4-atmosphere-remote-sensing/satellite-object-localization.
Analyzing Single Cell RNA Sequencing with Topological Nonnegative Matrix Factorization
Oct 24, 2023Abstract:Single-cell RNA sequencing (scRNA-seq) is a relatively new technology that has stimulated enormous interest in statistics, data science, and computational biology due to the high dimensionality, complexity, and large scale associated with scRNA-seq data. Nonnegative matrix factorization (NMF) offers a unique approach due to its meta-gene interpretation of resulting low-dimensional components. However, NMF approaches suffer from the lack of multiscale analysis. This work introduces two persistent Laplacian regularized NMF methods, namely, topological NMF (TNMF) and robust topological NMF (rTNMF). By employing a total of 12 datasets, we demonstrate that the proposed TNMF and rTNMF significantly outperform all other NMF-based methods. We have also utilized TNMF and rTNMF for the visualization of popular Uniform Manifold Approximation and Projection (UMAP) and t-distributed stochastic neighbor embedding (t-SNE).
K-Nearest-Neighbors Induced Topological PCA for scRNA Sequence Data Analysis
Oct 23, 2023



Abstract:Single-cell RNA sequencing (scRNA-seq) is widely used to reveal heterogeneity in cells, which has given us insights into cell-cell communication, cell differentiation, and differential gene expression. However, analyzing scRNA-seq data is a challenge due to sparsity and the large number of genes involved. Therefore, dimensionality reduction and feature selection are important for removing spurious signals and enhancing downstream analysis. Traditional PCA, a main workhorse in dimensionality reduction, lacks the ability to capture geometrical structure information embedded in the data, and previous graph Laplacian regularizations are limited by the analysis of only a single scale. We propose a topological Principal Components Analysis (tPCA) method by the combination of persistent Laplacian (PL) technique and L$_{2,1}$ norm regularization to address multiscale and multiclass heterogeneity issues in data. We further introduce a k-Nearest-Neighbor (kNN) persistent Laplacian technique to improve the robustness of our persistent Laplacian method. The proposed kNN-PL is a new algebraic topology technique which addresses the many limitations of the traditional persistent homology. Rather than inducing filtration via the varying of a distance threshold, we introduced kNN-tPCA, where filtrations are achieved by varying the number of neighbors in a kNN network at each step, and find that this framework has significant implications for hyper-parameter tuning. We validate the efficacy of our proposed tPCA and kNN-tPCA methods on 11 diverse benchmark scRNA-seq datasets, and showcase that our methods outperform other unsupervised PCA enhancements from the literature, as well as popular Uniform Manifold Approximation (UMAP), t-Distributed Stochastic Neighbor Embedding (tSNE), and Projection Non-Negative Matrix Factorization (NMF) by significant margins.
Analyzing scRNA-seq data by CCP-assisted UMAP and t-SNE
Jun 23, 2023Abstract:Single-cell RNA sequencing (scRNA-seq) is widely used to reveal heterogeneity in cells, which has given us insights into cell-cell communication, cell differentiation, and differential gene expression. However, analyzing scRNA-seq data is a challenge due to sparsity and the large number of genes involved. Therefore, dimensionality reduction and feature selection are important for removing spurious signals and enhancing downstream analysis. Correlated clustering and projection (CCP) was recently introduced as an effective method for preprocessing scRNA-seq data. CCP utilizes gene-gene correlations to partition the genes and, based on the partition, employs cell-cell interactions to obtain super-genes. Because CCP is a data-domain approach that does not require matrix diagonalization, it can be used in many downstream machine learning tasks. In this work, we utilize CCP as an initialization tool for uniform manifold approximation and projection (UMAP) and t-distributed stochastic neighbor embedding (t-SNE). By using eight publicly available datasets, we have found that CCP significantly improves UMAP and t-SNE visualization and dramatically improve their accuracy.
CCP: Correlated Clustering and Projection for Dimensionality Reduction
Jun 08, 2022



Abstract:Most dimensionality reduction methods employ frequency domain representations obtained from matrix diagonalization and may not be efficient for large datasets with relatively high intrinsic dimensions. To address this challenge, Correlated Clustering and Projection (CCP) offers a novel data domain strategy that does not need to solve any matrix. CCP partitions high-dimensional features into correlated clusters and then projects correlated features in each cluster into a one-dimensional representation based on sample correlations. Residue-Similarity (R-S) scores and indexes, the shape of data in Riemannian manifolds, and algebraic topology-based persistent Laplacian are introduced for visualization and analysis. Proposed methods are validated with benchmark datasets associated with various machine learning algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge