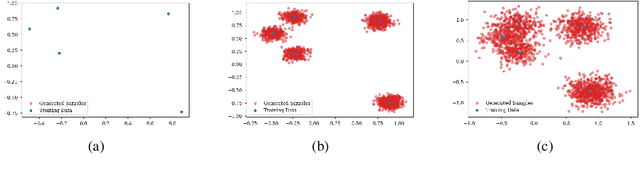
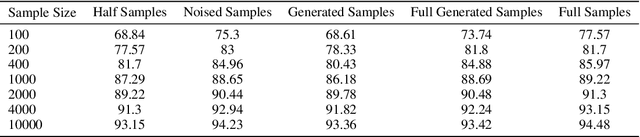
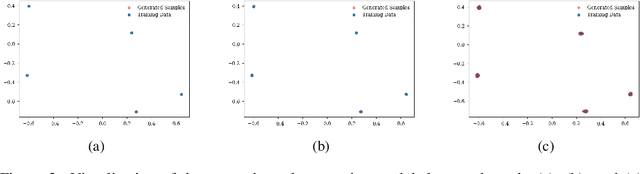
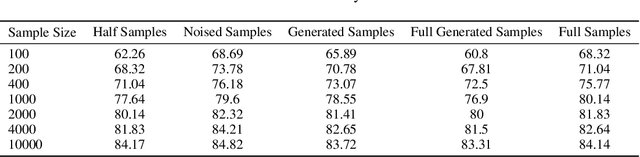
Generation Properties of Stochastic Interpolation under Finite Training Set

This paper investigates the theoretical behavior of generative models under finite training populations. Within the stochastic interpolation generative framework, we derive closed-form expressions for the optimal velocity field and score function when only a finite number of training samples are available. We demonstrate that, under some regularity conditions, the deterministic generative process exactly recovers the training samples, while the stochastic generative process manifests as training samples with added Gaussian noise. Beyond the idealized setting, we consider model estimation errors and introduce formal definitions of underfitting and overfitting specific to generative models. Our theoretical analysis reveals that, in the presence of estimation errors, the stochastic generation process effectively produces convex combinations of training samples corrupted by a mixture of uniform and Gaussian noise. Experiments on generation tasks and downstream tasks such as classification support our theory.

SPD-DDPM: Denoising Diffusion Probabilistic Models in the Symmetric Positive Definite Space

Symmetric positive definite~(SPD) matrices have shown important value and applications in statistics and machine learning, such as FMRI analysis and traffic prediction. Previous works on SPD matrices mostly focus on discriminative models, where predictions are made directly on $E(X|y)$, where $y$ is a vector and $X$ is an SPD matrix. However, these methods are challenging to handle for large-scale data, as they need to access and process the whole data. In this paper, inspired by denoising diffusion probabilistic model~(DDPM), we propose a novel generative model, termed SPD-DDPM, by introducing Gaussian distribution in the SPD space to estimate $E(X|y)$. Moreover, our model is able to estimate $p(X)$ unconditionally and flexibly without giving $y$. On the one hand, the model conditionally learns $p(X|y)$ and utilizes the mean of samples to obtain $E(X|y)$ as a prediction. On the other hand, the model unconditionally learns the probability distribution of the data $p(X)$ and generates samples that conform to this distribution. Furthermore, we propose a new SPD net which is much deeper than the previous networks and allows for the inclusion of conditional factors. Experiment results on toy data and real taxi data demonstrate that our models effectively fit the data distribution both unconditionally and unconditionally and provide accurate predictions.