A Fast and Efficient Stochastic Opposition-Based Learning for Differential Evolution in Numerical Optimization

A new variant of stochastic opposition-based learning (OBL) is proposed in this paper. OBL is a relatively new machine learning concept, which consists of simultaneously calculating an original solution and its opposite to accelerate the convergence of soft computing algorithms. Recently a new opposition-based differential evolution (ODE) variant called BetaCODE was proposed as a combination of differential evolution and a new stochastic OBL variant called BetaCOBL. BetaCOBL is capable of flexibly adjusting the probability density functions used to calculate opposite solutions, generating more diverse opposite solutions, and preventing the waste of fitness evaluations. While it has shown outstanding performance compared to several state-of-the-art OBL variants, BetaCOBL is challenging with more complex problems because of its high computational cost. Besides, as it assumes that the decision variables are independent, there is a limitation in the search for decent opposite solutions on inseparable problems. In this paper, we propose an improved stochastic OBL variant that mitigates all the limitations of BetaCOBL. The proposed algorithm called iBetaCOBL reduces the computational cost from $O(NP^{2} \cdot D)$ to $O(NP \cdot D)$ ($NP$ and $D$ stand for population size and dimension, respectively) using a linear time diversity measure. In addition, iBetaCOBL preserves the strongly dependent decision variables that are adjacent to each other using the multiple exponential crossover. The results of the performance evaluations on a set of 58 test functions show that iBetaCODE finds more accurate solutions than ten state-of-the-art ODE variants including BetaCODE. Additionally, we applied iBetaCOBL to two state-of-the-art DE variants, and as in the previous results, iBetaCOBL based variants exhibit significantly improved performance.

ACM-DE: Adaptive p-best Cauchy Mutation with linear failure threshold reduction for Differential Evolution in numerical optimization

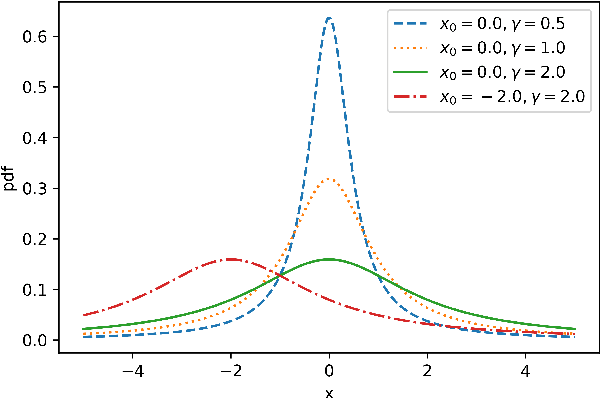
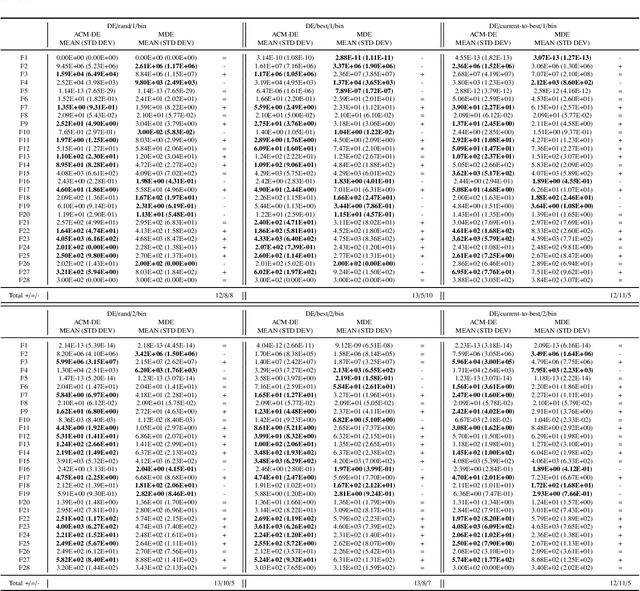
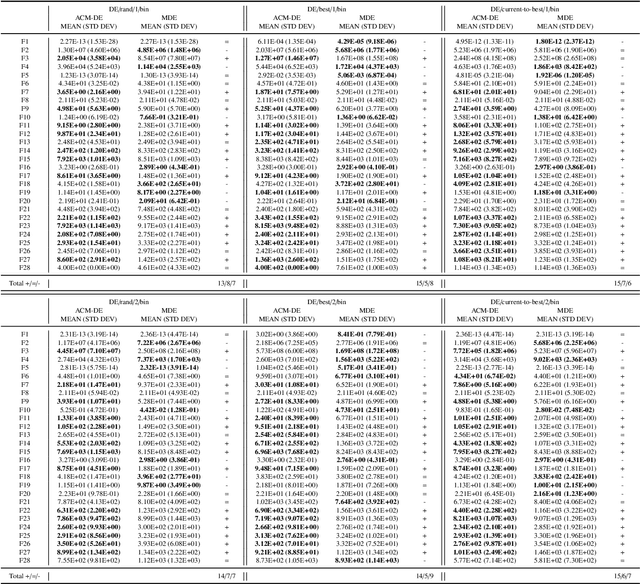
Differential evolution (DE) is an efficient evolutionary algorithm for optimizing continuous optimization problems. Although DE has been successfully applied to various real-world problems, it suffers from premature convergence where all individuals converge to a suboptimal solution too early. To address this problem, modified DE that uses the Cauchy mutation was proposed, but it has serious limitations of 1) controlling the balance between exploration and exploitation; 2) adjusting the algorithm to a given problem; 3) having less reliable performance on multimodal problems. In this paper, we propose a new adaptive Cauchy mutation based DE variant called ACM-DE (Adaptive Cauchy Mutation Differential Evolution), which removes all of these limitations. Specifically, two popular parameter controls are employed for the exploration and exploitation scheme and robust performance. Also, a less greedy approach is employed, which uses any of the top p% individuals in the phase of the Cauchy mutation. Experimental results on a set of 58 benchmark problems show that ACM-DE is capable of finding more accurate solutions than modified DE, especially for multimodal problems. In addition, we applied ACM to two state-of-the-art DE variants, and similar to the previous results, ACM based variants exhibit significantly improved performance.