ACM-DE: Adaptive p-best Cauchy Mutation with linear failure threshold reduction for Differential Evolution in numerical optimization

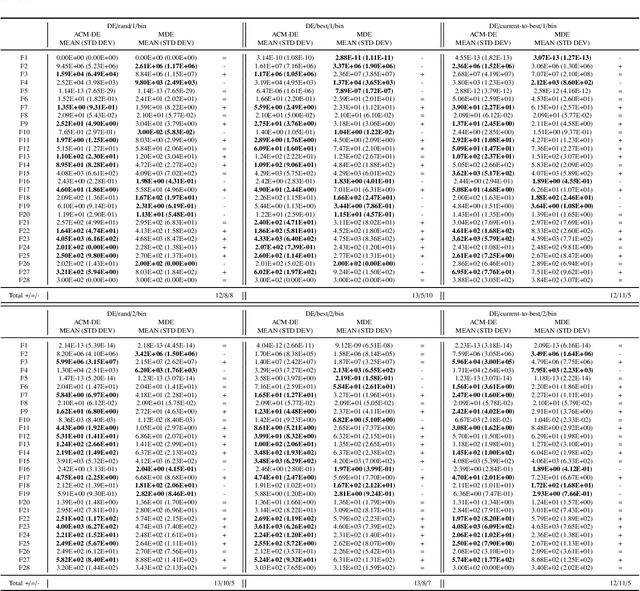
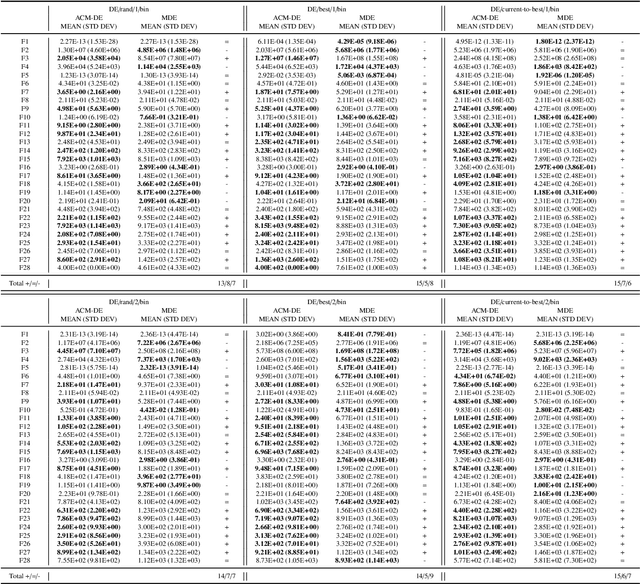
Differential evolution (DE) is an efficient evolutionary algorithm for optimizing continuous optimization problems. Although DE has been successfully applied to various real-world problems, it suffers from premature convergence where all individuals converge to a suboptimal solution too early. To address this problem, modified DE that uses the Cauchy mutation was proposed, but it has serious limitations of 1) controlling the balance between exploration and exploitation; 2) adjusting the algorithm to a given problem; 3) having less reliable performance on multimodal problems. In this paper, we propose a new adaptive Cauchy mutation based DE variant called ACM-DE (Adaptive Cauchy Mutation Differential Evolution), which removes all of these limitations. Specifically, two popular parameter controls are employed for the exploration and exploitation scheme and robust performance. Also, a less greedy approach is employed, which uses any of the top p% individuals in the phase of the Cauchy mutation. Experimental results on a set of 58 benchmark problems show that ACM-DE is capable of finding more accurate solutions than modified DE, especially for multimodal problems. In addition, we applied ACM to two state-of-the-art DE variants, and similar to the previous results, ACM based variants exhibit significantly improved performance.