Non-expert to Expert Motion Translation Using Generative Adversarial Networks

Decreasing skilled workers is a very serious problem in the world. To deal with this problem, the skill transfer from experts to robots has been researched. These methods which teach robots by human motion are called imitation learning. Experts' skills generally appear in not only position data, but also force data. Thus, position and force data need to be saved and reproduced. To realize this, a lot of research has been conducted in the framework of a motion-copying system. Recent research uses machine learning methods to generate motion commands. However, most of them could not change tasks by following human intention. Some of them can change tasks by conditional training, but the labels are limited. Thus, we propose the flexible motion translation method by using Generative Adversarial Networks. The proposed method enables users to teach robots tasks by inputting data, and skills by a trained model. We evaluated the proposed system with a 3-DOF calligraphy robot.

Evaluating generation of chaotic time series by convolutional generative adversarial networks

To understand the ability and limitations of convolutional neural networks to generate time series that mimic complex temporal signals, we trained a generative adversarial network consisting of deep convolutional networks to generate chaotic time series and used nonlinear time series analysis to evaluate the generated time series. A numerical measure of determinism and the Lyapunov exponent, a measure of trajectory instability, showed that the generated time series well reproduce the chaotic properties of the original time series. However, error distribution analyses showed that large errors appeared at a low but non-negligible rate. Such errors would not be expected if the distribution were assumed to be exponential.

Non-iterative optimization of pseudo-labeling thresholds for training object detection models from multiple datasets

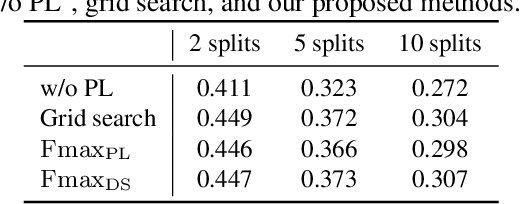
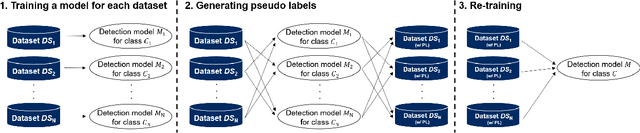
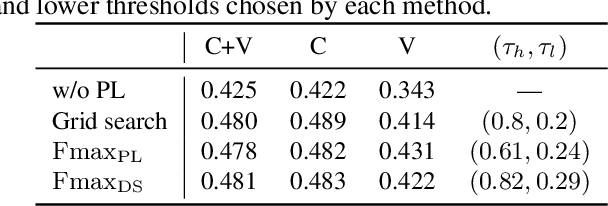
We propose a non-iterative method to optimize pseudo-labeling thresholds for learning object detection from a collection of low-cost datasets, each of which is annotated for only a subset of all the object classes. A popular approach to this problem is first to train teacher models and then to use their confident predictions as pseudo ground-truth labels when training a student model. To obtain the best result, however, thresholds for prediction confidence must be adjusted. This process typically involves iterative search and repeated training of student models and is time-consuming. Therefore, we develop a method to optimize the thresholds without iterative optimization by maximizing the $F_\beta$-score on a validation dataset, which measures the quality of pseudo labels and can be measured without training a student model. We experimentally demonstrate that our proposed method achieves an mAP comparable to that of grid search on the COCO and VOC datasets.